动态规划解题思路¶

上两节介绍了动态规划问题的主要特征，接下来我们一起探究两个更加实用的问题。

如何判断一个问题是不是动态规划问题？
求解动态规划问题该从何处入手，完整步骤是什么？

问题判断¶

总的来说，如果一个问题包含重叠子问题、最优子结构，并满足无后效性，那么它通常适合用动态规划求解。然而，我们很难从问题描述中直接提取出这些特性。因此我们通常会放宽条件，先观察问题是否适合使用回溯（穷举）解决。

适合用回溯解决的问题通常满足“决策树模型”，这种问题可以使用树形结构来描述，其中每一个节点代表一个决策，每一条路径代表一个决策序列。

换句话说，如果问题包含明确的决策概念，并且解是通过一系列决策产生的，那么它就满足决策树模型，通常可以使用回溯来解决。

在此基础上，动态规划问题还有一些判断的“加分项”。

问题包含最大（小）或最多（少）等最优化描述。
问题的状态能够使用一个列表、多维矩阵或树来表示，并且一个状态与其周围的状态存在递推关系。

相应地，也存在一些“减分项”。

问题的目标是找出所有可能的解决方案，而不是找出最优解。
问题描述中有明显的排列组合的特征，需要返回具体的多个方案。

如果一个问题满足决策树模型，并具有较为明显的“加分项”，我们就可以假设它是一个动态规划问题，并在求解过程中验证它。

问题求解步骤¶

动态规划的解题流程会因问题的性质和难度而有所不同，但通常遵循以下步骤：描述决策，定义状态，建立 $dp$ 表，推导状态转移方程，确定边界条件等。

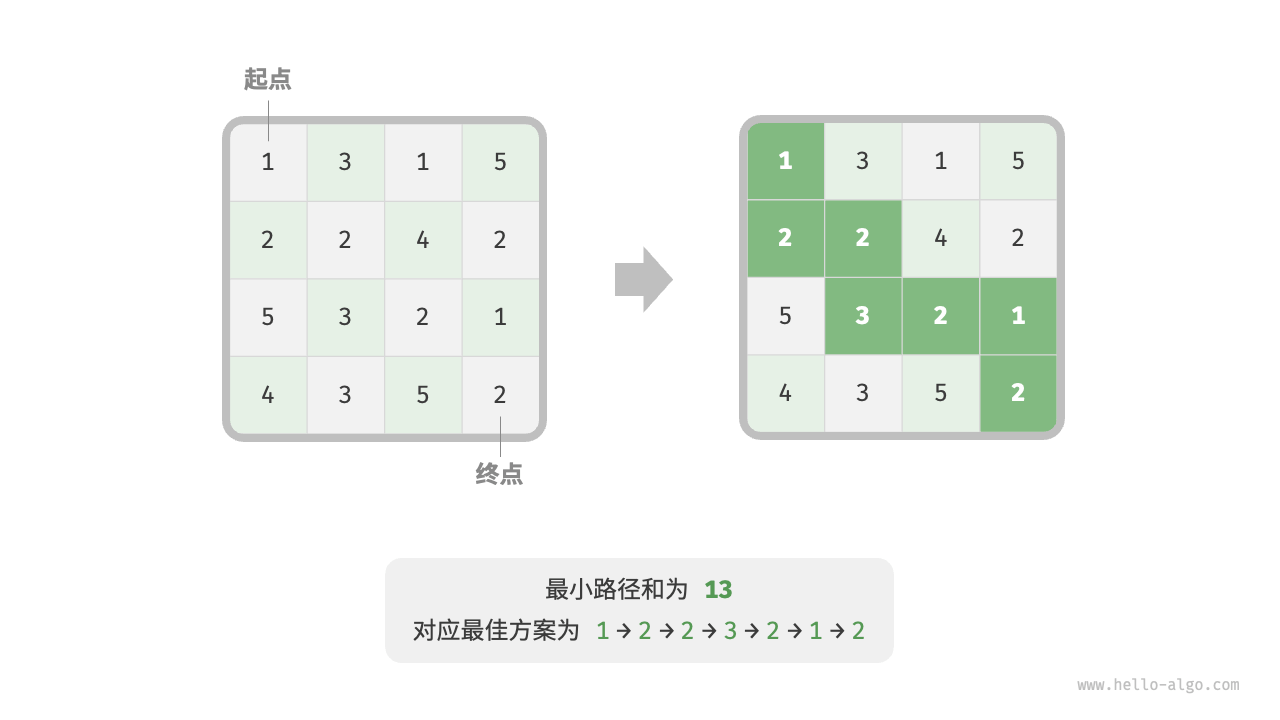
为了更形象地展示解题步骤，我们使用一个经典问题“最小路径和”来举例。

Question

给定一个 $n \times m$ 的二维网格 grid ，网格中的每个单元格包含一个非负整数，表示该单元格的代价。机器人以左上角单元格为起始点，每次只能向下或者向右移动一步，直至到达右下角单元格。请返回从左上角到右下角的最小路径和。

下图展示了一个例子，给定网格的最小路径和为 $13$ 。

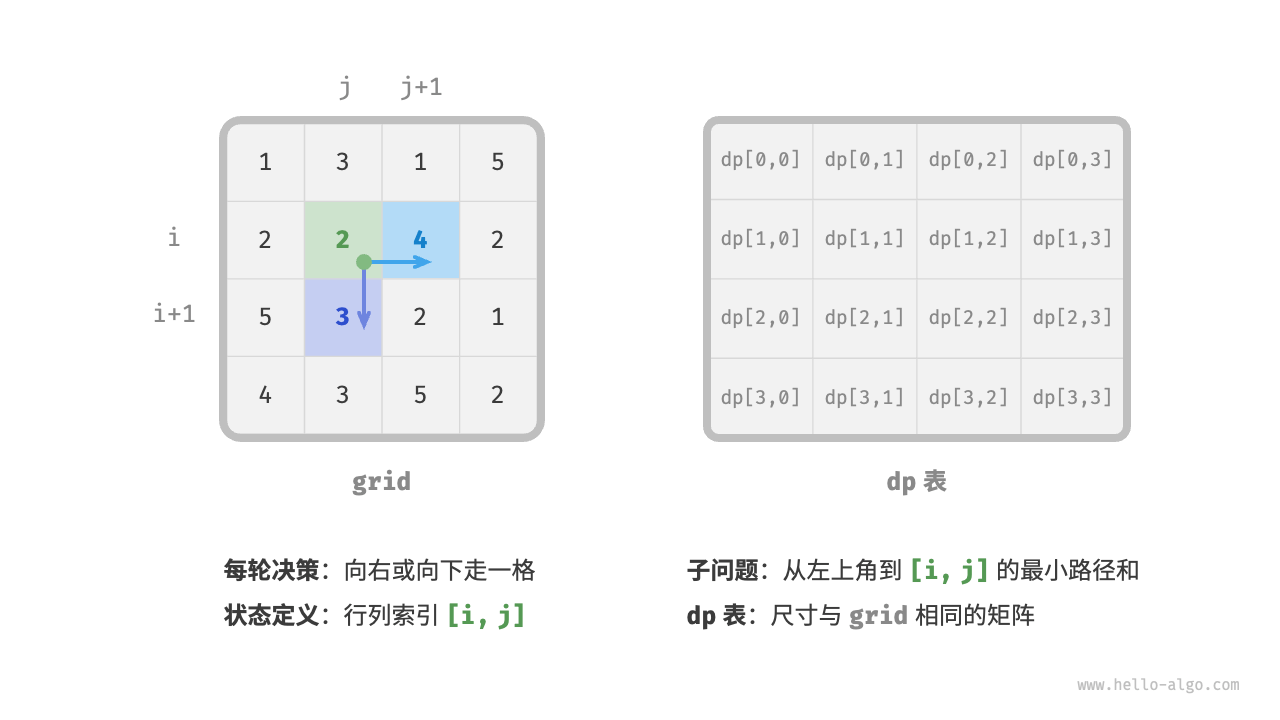
第一步：思考每轮的决策，定义状态，从而得到 $dp$ 表

本题的每一轮的决策就是从当前格子向下或向右走一步。设当前格子的行列索引为 $[i, j]$ ，则向下或向右走一步后，索引变为 $[i+1, j]$ 或 $[i, j+1]$ 。因此，状态应包含行索引和列索引两个变量，记为 $[i, j]$ 。

状态 $[i, j]$ 对应的子问题为：从起始点 $[0, 0]$ 走到 $[i, j]$ 的最小路径和，解记为 $dp[i, j]$ 。

至此，我们就得到了下图所示的二维 $dp$ 矩阵，其尺寸与输入网格 $grid$ 相同。

Note

动态规划和回溯过程可以描述为一个决策序列，而状态由所有决策变量构成。它应当包含描述解题进度的所有变量，其包含了足够的信息，能够用来推导出下一个状态。

每个状态都对应一个子问题，我们会定义一个 $dp$ 表来存储所有子问题的解，状态的每个独立变量都是 $dp$ 表的一个维度。从本质上看，$dp$ 表是状态和子问题的解之间的映射。

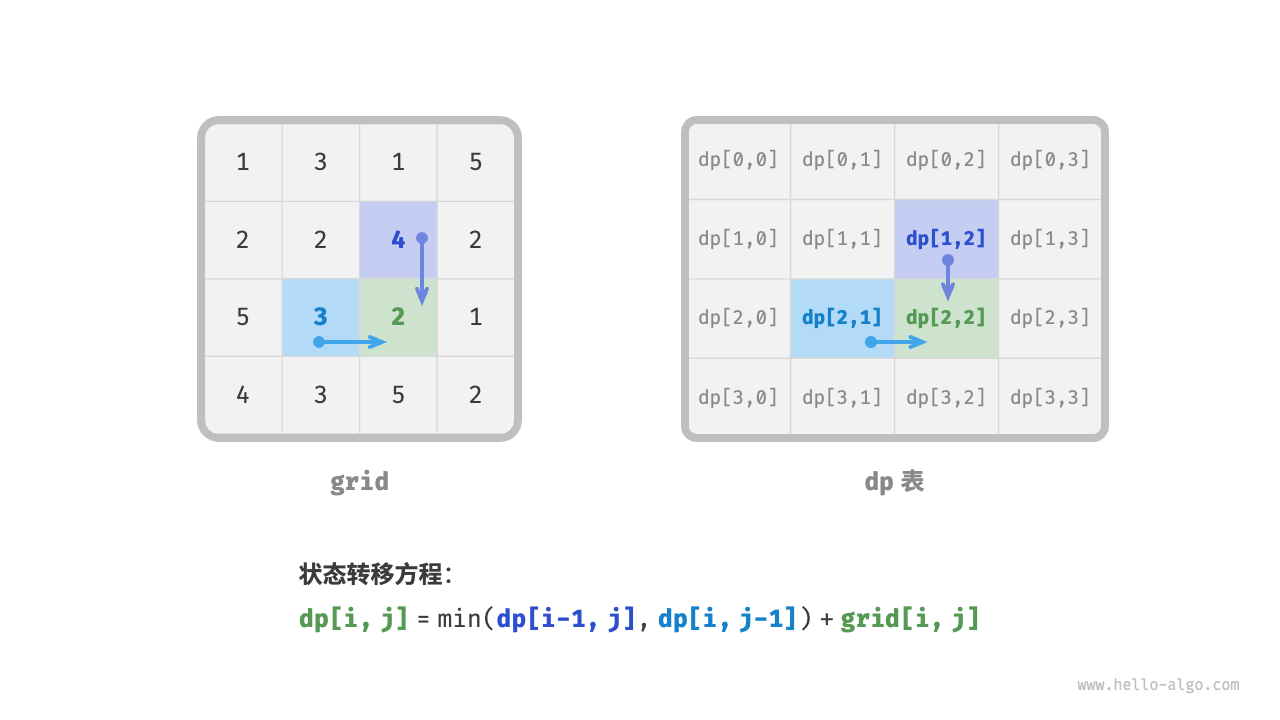
第二步：找出最优子结构，进而推导出状态转移方程

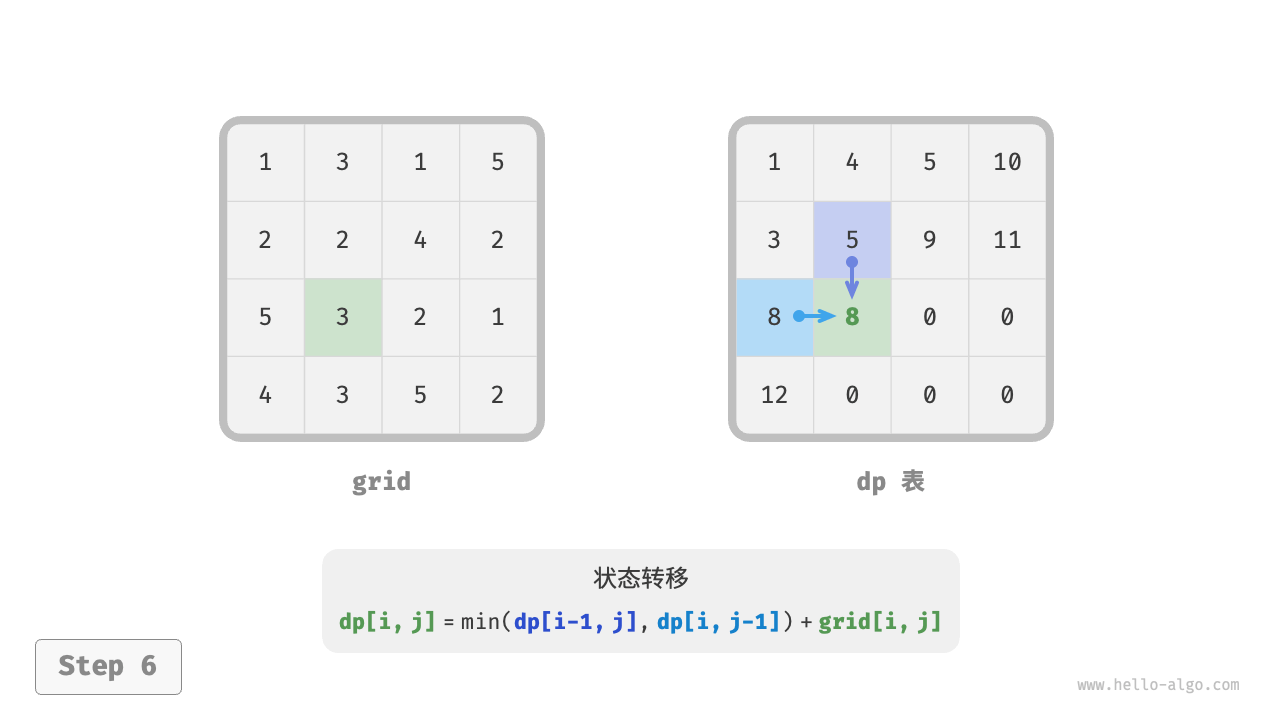
对于状态 $[i, j]$ ，它只能从上边格子 $[i-1, j]$ 和左边格子 $[i, j-1]$ 转移而来。因此最优子结构为：到达 $[i, j]$ 的最小路径和由 $[i, j-1]$ 的最小路径和与 $[i-1, j]$ 的最小路径和中较小的那一个决定。

根据以上分析，可推出下图所示的状态转移方程：

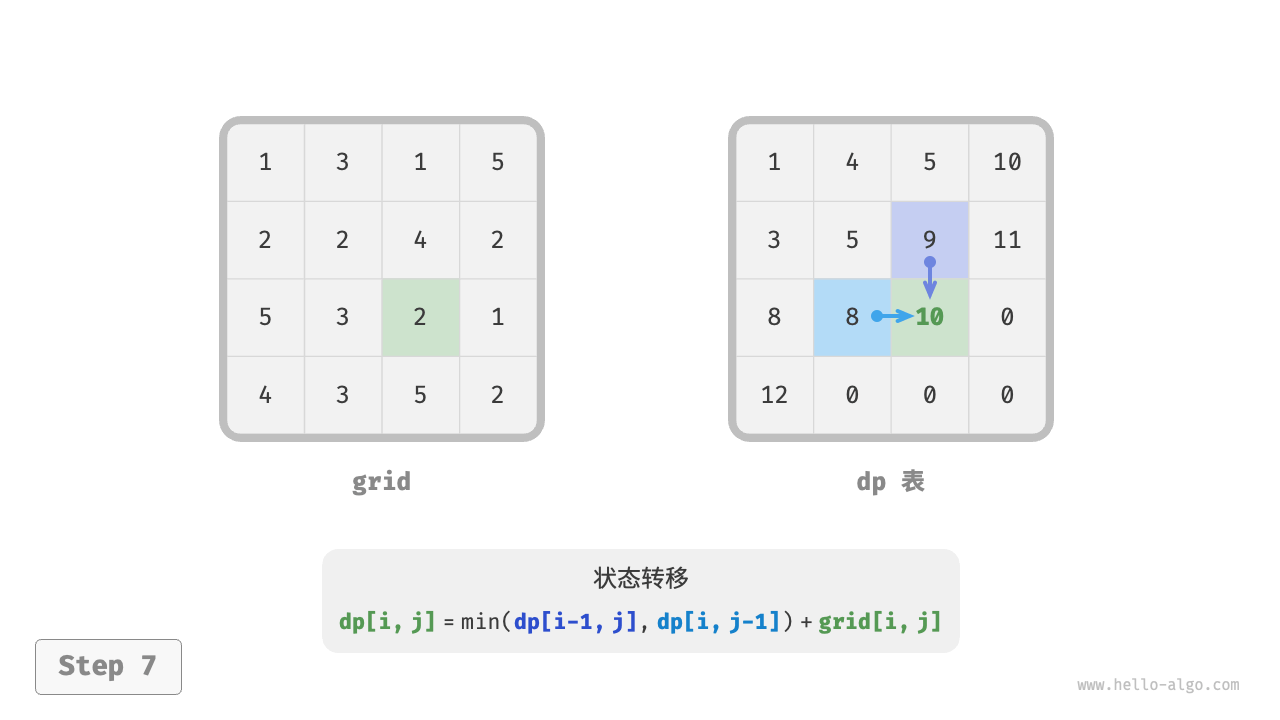
$$ dp[i, j] = \min(dp[i-1, j], dp[i, j-1]) + grid[i, j] $$

Note

根据定义好的 $dp$ 表，思考原问题和子问题的关系，找出通过子问题的最优解来构造原问题的最优解的方法，即最优子结构。

一旦我们找到了最优子结构，就可以使用它来构建出状态转移方程。

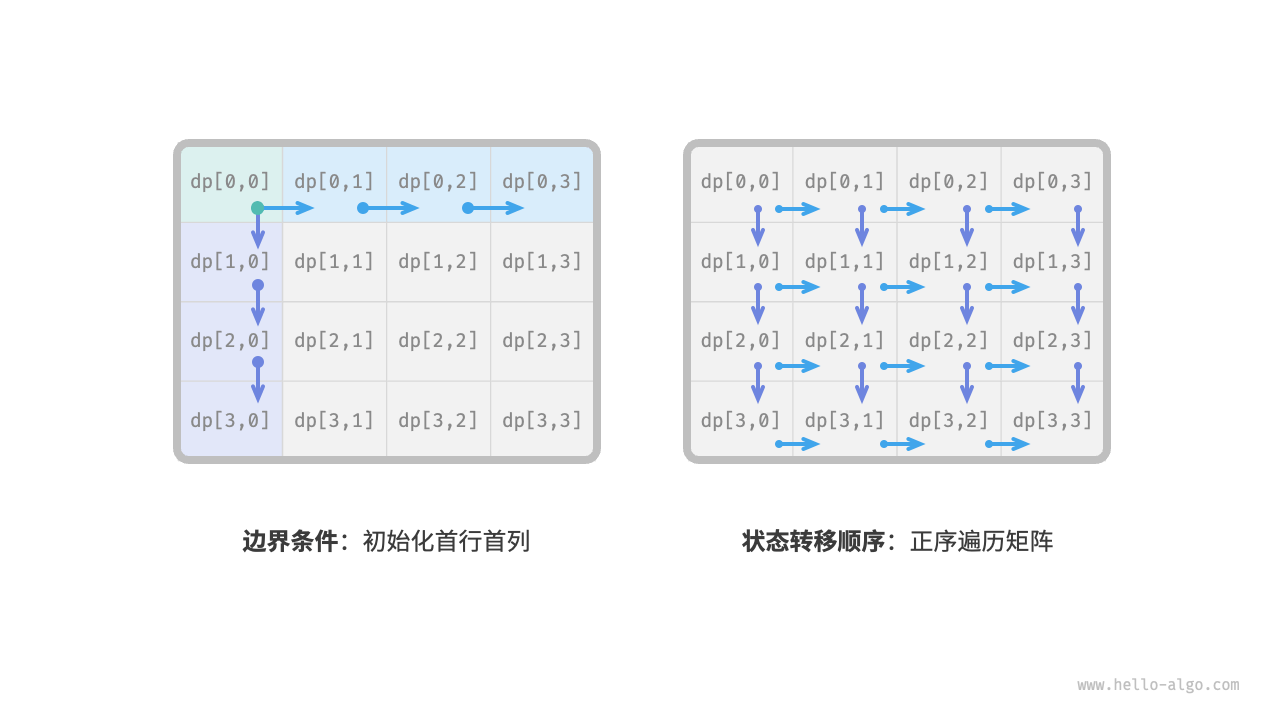
第三步：确定边界条件和状态转移顺序

在本题中，处在首行的状态只能从其左边的状态得来，处在首列的状态只能从其上边的状态得来，因此首行 $i = 0$ 和首列 $j = 0$ 是边界条件。

如下图所示，由于每个格子是由其左方格子和上方格子转移而来，因此我们使用循环来遍历矩阵，外循环遍历各行，内循环遍历各列。

Note

边界条件在动态规划中用于初始化 $dp$ 表，在搜索中用于剪枝。

状态转移顺序的核心是要保证在计算当前问题的解时，所有它依赖的更小子问题的解都已经被正确地计算出来。

根据以上分析，我们已经可以直接写出动态规划代码。然而子问题分解是一种从顶至底的思想，因此按照“暴力搜索 $\rightarrow$ 记忆化搜索 $\rightarrow$ 动态规划”的顺序实现更加符合思维习惯。

方法一：暴力搜索¶

从状态 $[i, j]$ 开始搜索，不断分解为更小的状态 $[i-1, j]$ 和 $[i, j-1]$ ，递归函数包括以下要素。

递归参数：状态 $[i, j]$ 。
返回值：从 $[0, 0]$ 到 $[i, j]$ 的最小路径和 $dp[i, j]$ 。
终止条件：当 $i = 0$ 且 $j = 0$ 时，返回代价 $grid[0, 0]$ 。
剪枝：当 $i < 0$ 时或 $j < 0$ 时索引越界，此时返回代价 $+\infty$ ，代表不可行。

实现代码如下：

[file]{min_path_sum}-[class]{}-[func]{min_path_sum_dfs}

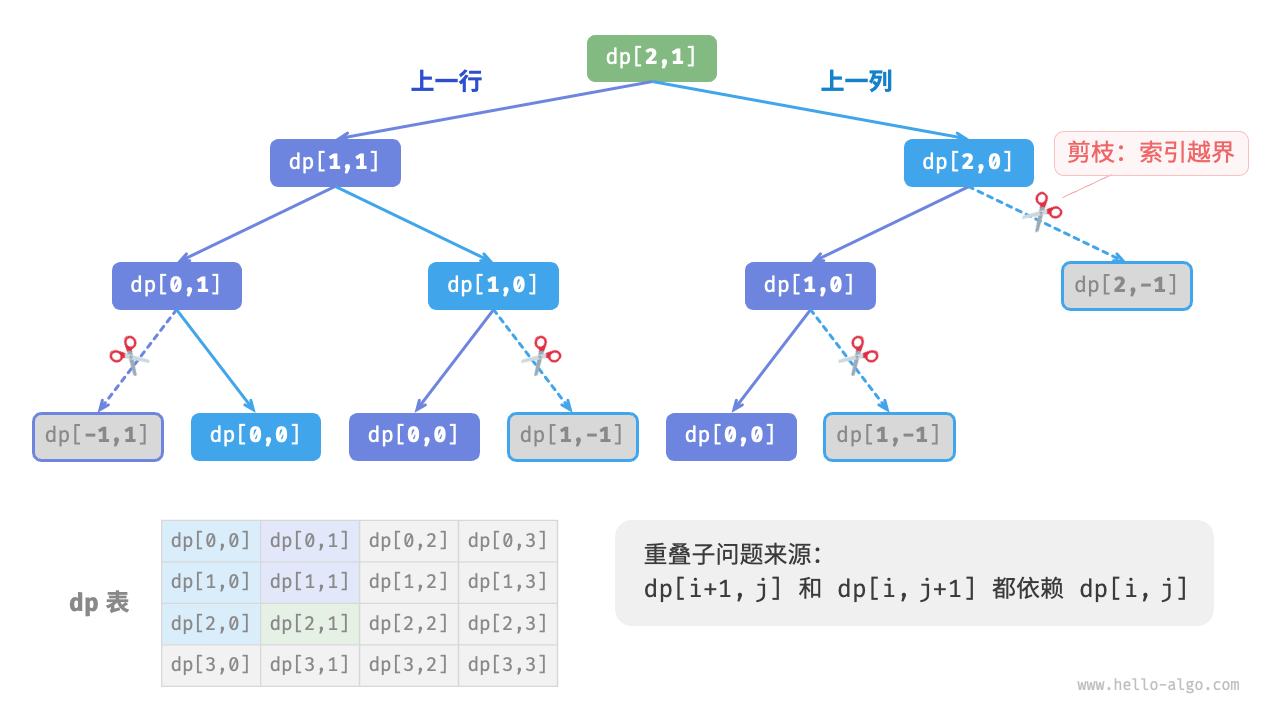
下图给出了以 $dp[2, 1]$ 为根节点的递归树，其中包含一些重叠子问题，其数量会随着网格 grid 的尺寸变大而急剧增多。

从本质上看，造成重叠子问题的原因为：存在多条路径可以从左上角到达某一单元格。

每个状态都有向下和向右两种选择，从左上角走到右下角总共需要 $m + n - 2$ 步，所以最差时间复杂度为 $O(2^{m + n})$ 。请注意，这种计算方式未考虑临近网格边界的情况，当到达网络边界时只剩下一种选择，因此实际的路径数量会少一些。

方法二：记忆化搜索¶

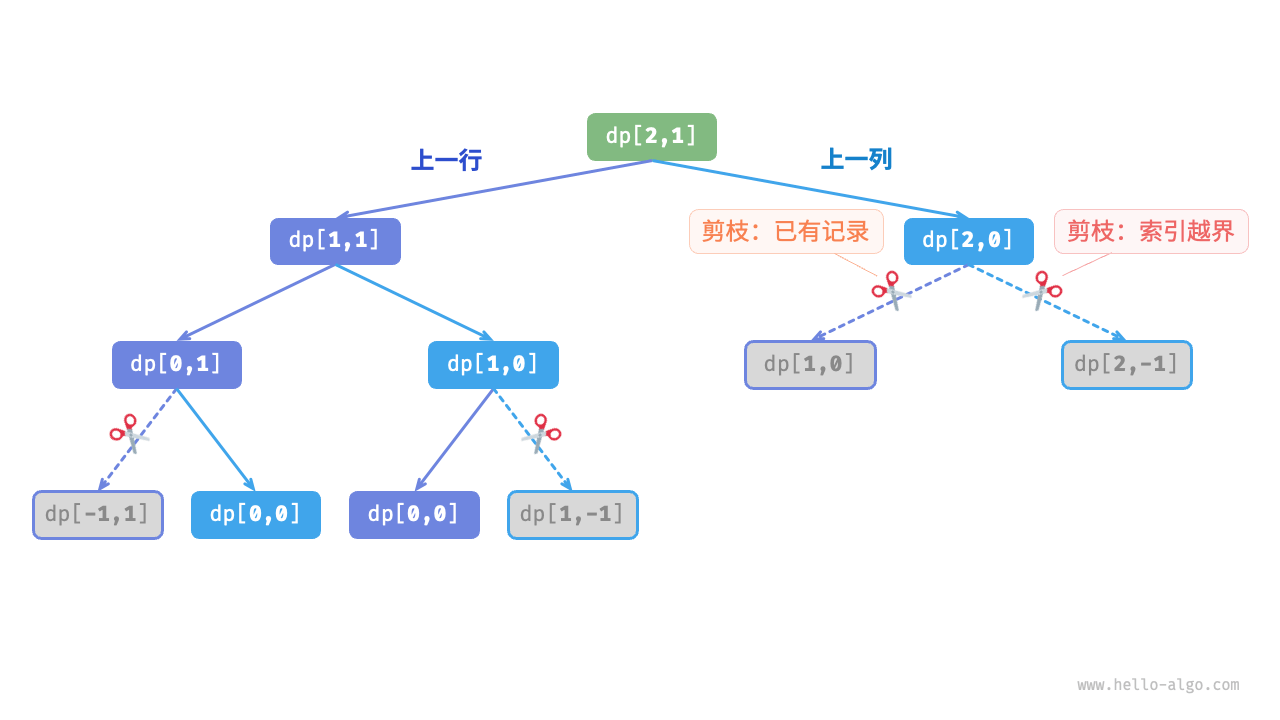
我们引入一个和网格 grid 相同尺寸的记忆列表 mem ，用于记录各个子问题的解，并将重叠子问题进行剪枝：

[file]{min_path_sum}-[class]{}-[func]{min_path_sum_dfs_mem}

如下图所示，在引入记忆化后，所有子问题的解只需计算一次，因此时间复杂度取决于状态总数，即网格尺寸 $O(nm)$ 。

方法三：动态规划¶

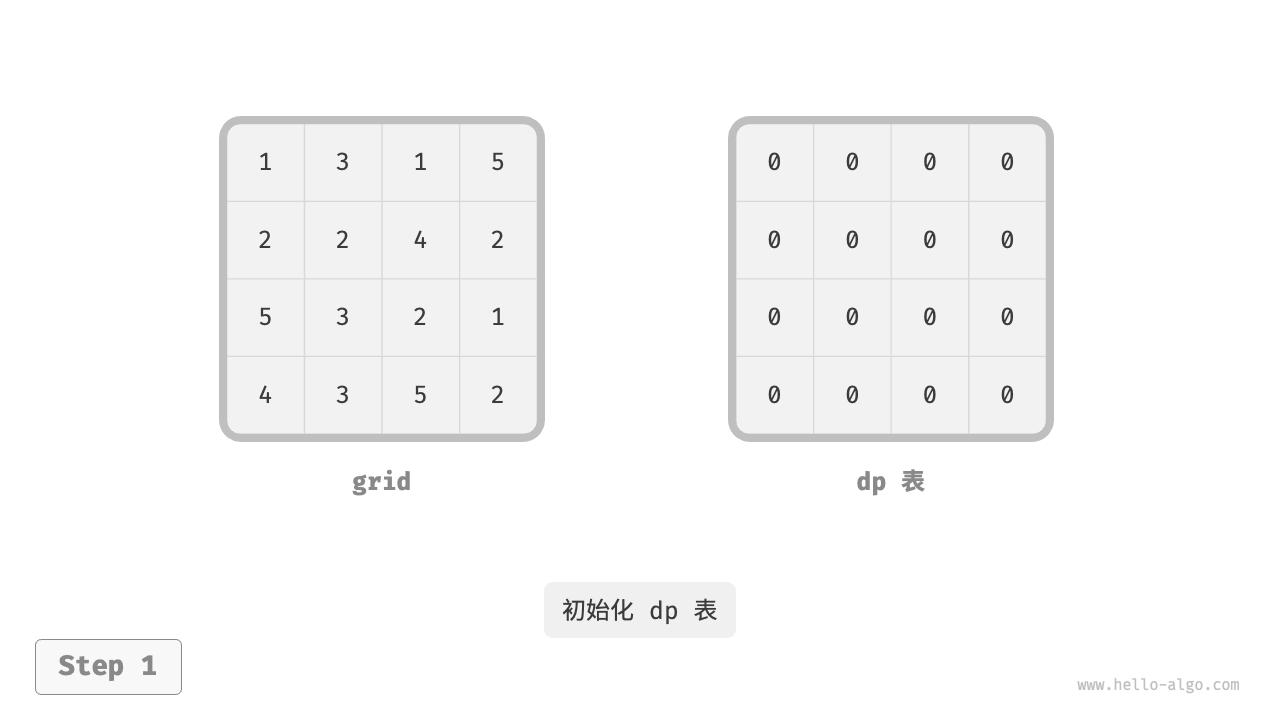
基于迭代实现动态规划解法，代码如下所示：

[file]{min_path_sum}-[class]{}-[func]{min_path_sum_dp}

下图展示了最小路径和的状态转移过程，其遍历了整个网格，因此时间复杂度为 $O(nm)$ 。

数组 dp 大小为 $n \times m$ ，因此空间复杂度为 $O(nm)$ 。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

=== "<7>"

=== "<8>"

=== "<9>"

=== "<10>"

=== "<11>"

=== "<12>"

空间优化¶

由于每个格子只与其左边和上边的格子有关，因此我们可以只用一个单行数组来实现 $dp$ 表。

请注意，因为数组 dp 只能表示一行的状态，所以我们无法提前初始化首列状态，而是在遍历每行时更新它：

[file]{min_path_sum}-[class]{}-[func]{min_path_sum_dp_comp}