归并排序¶
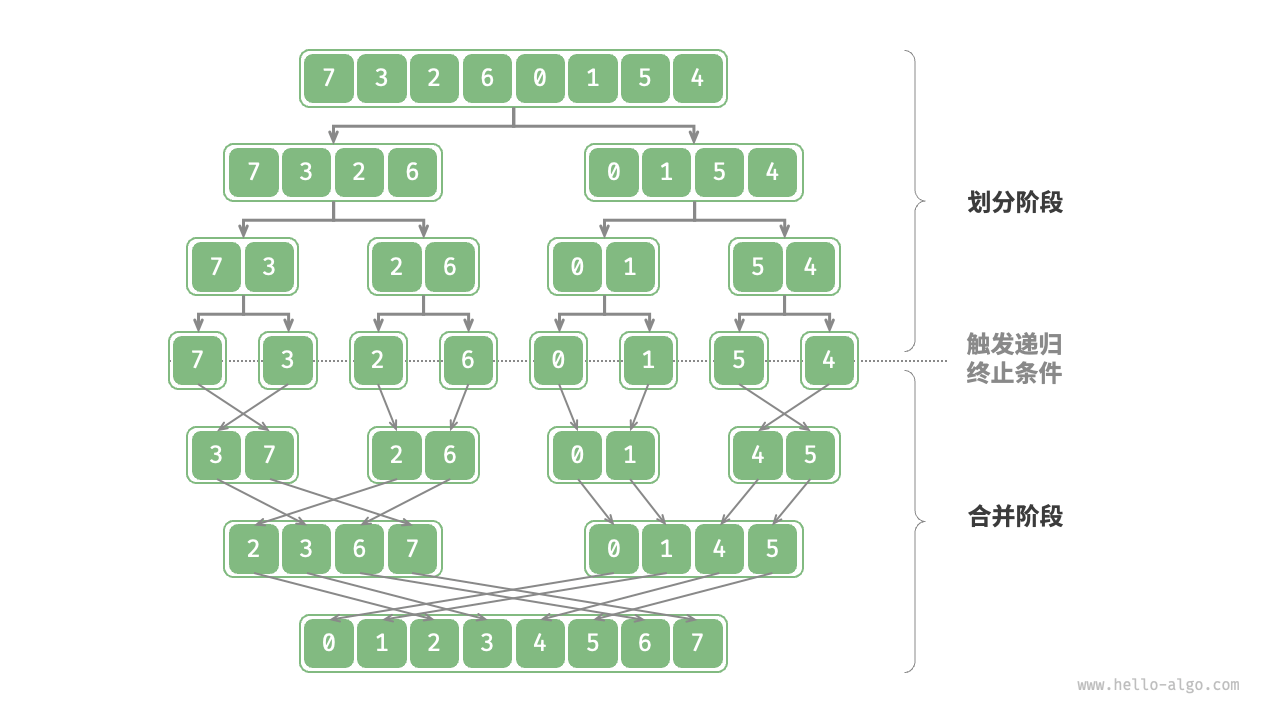
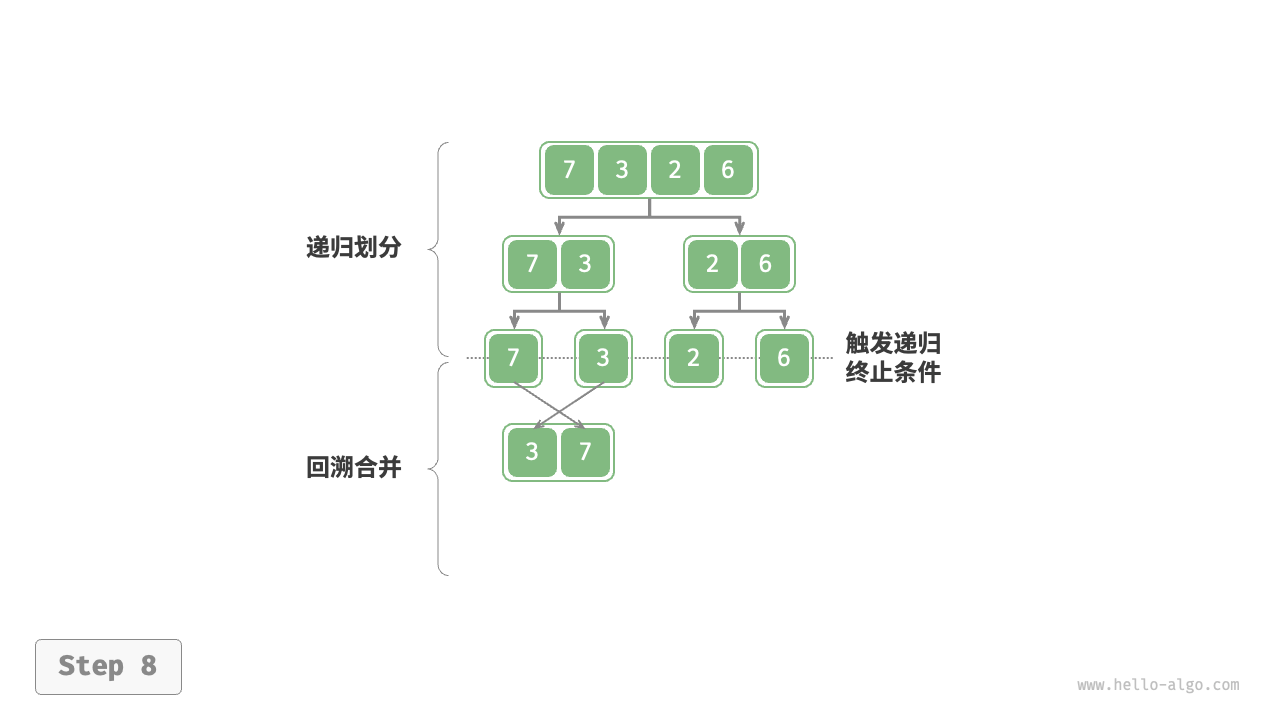
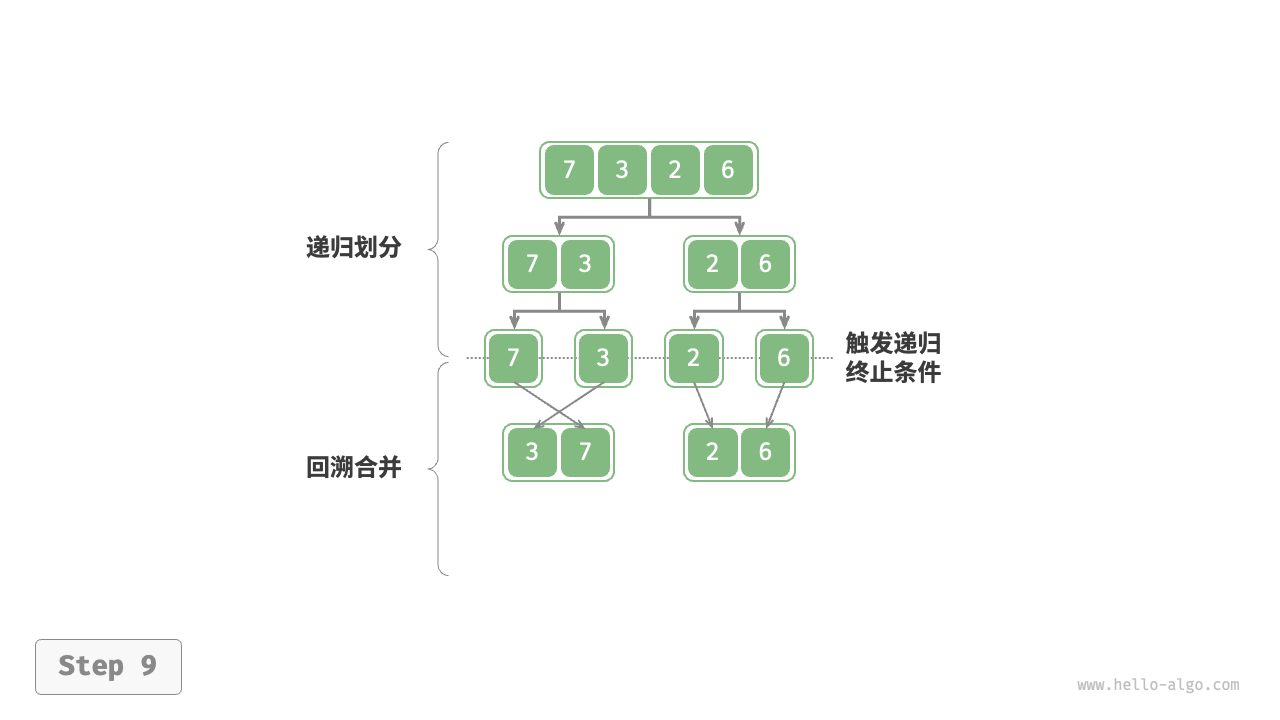
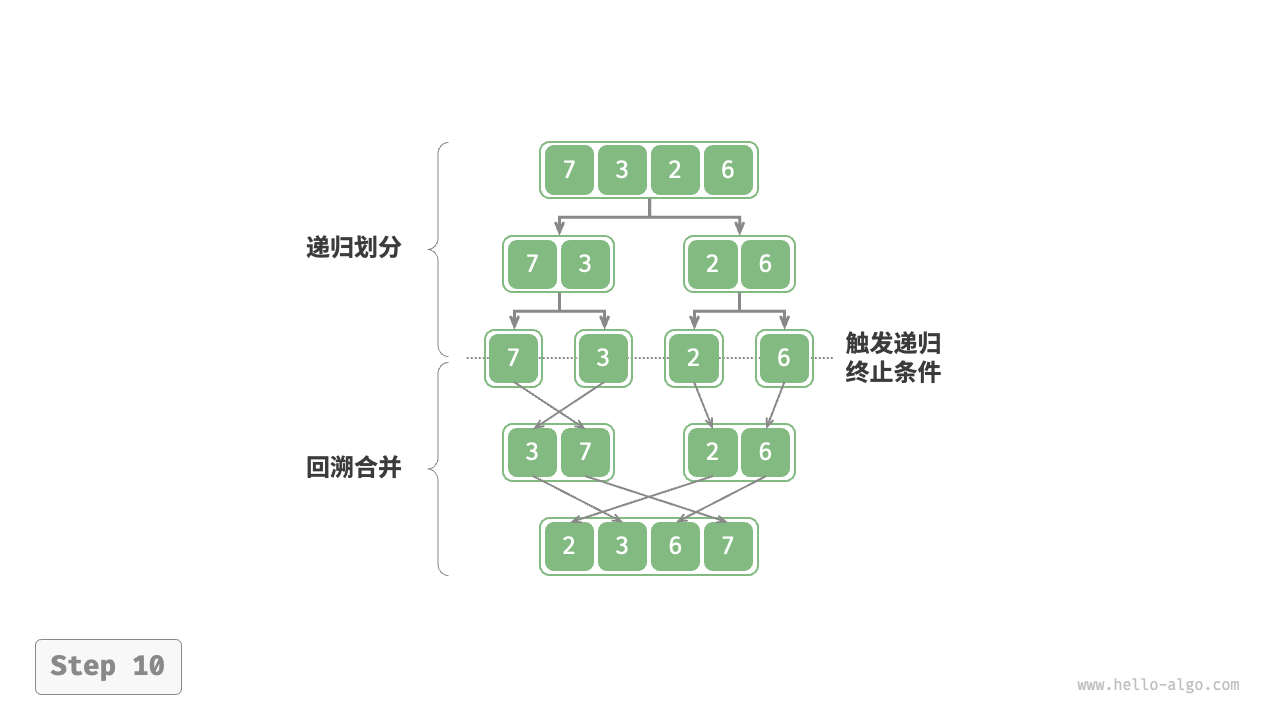
归并排序(merge sort)是一种基于分治策略的排序算法,包含下图所示的“划分”和“合并”阶段。
- 划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题。
- 合并阶段:当子数组长度为 1 时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较长的有序数组,直至结束。
算法流程¶
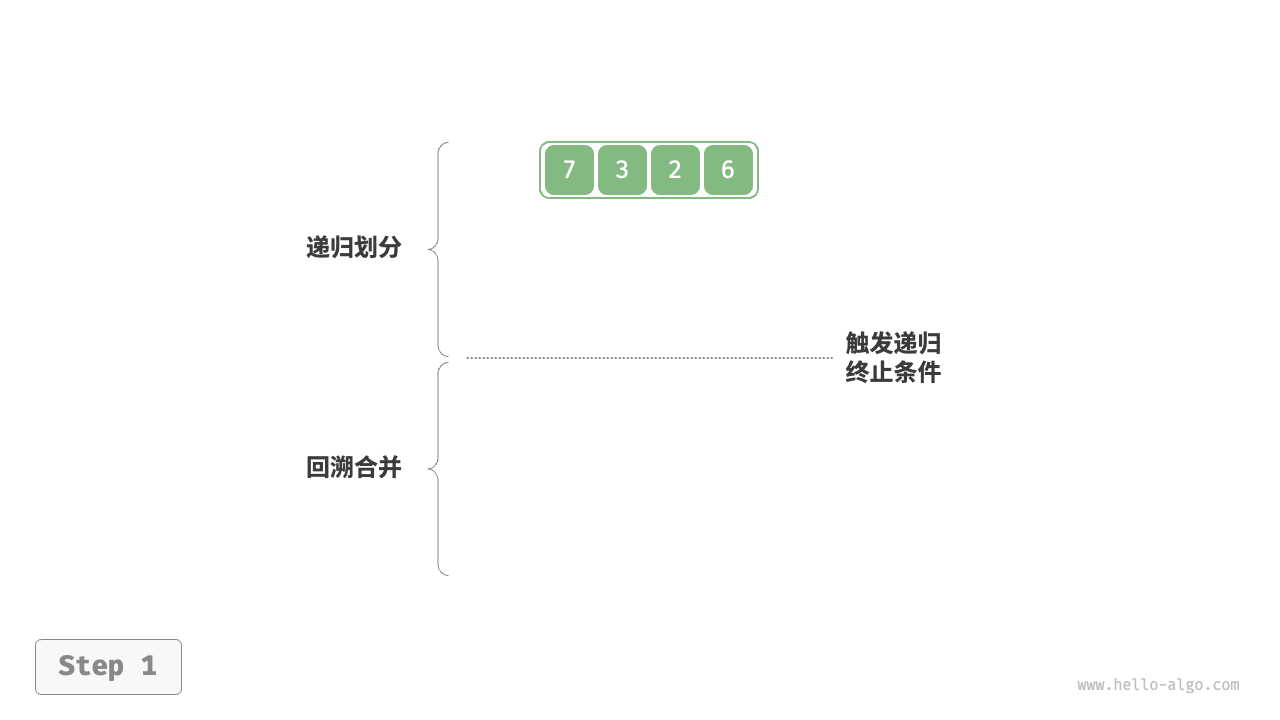
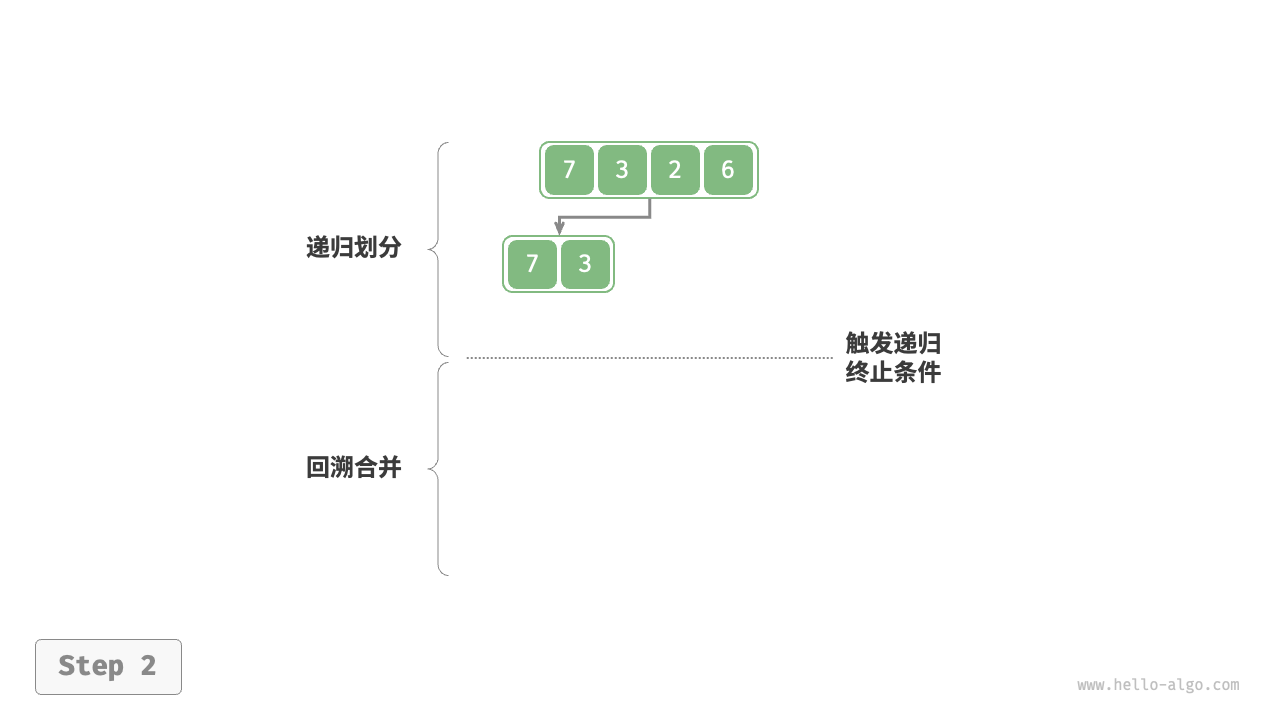
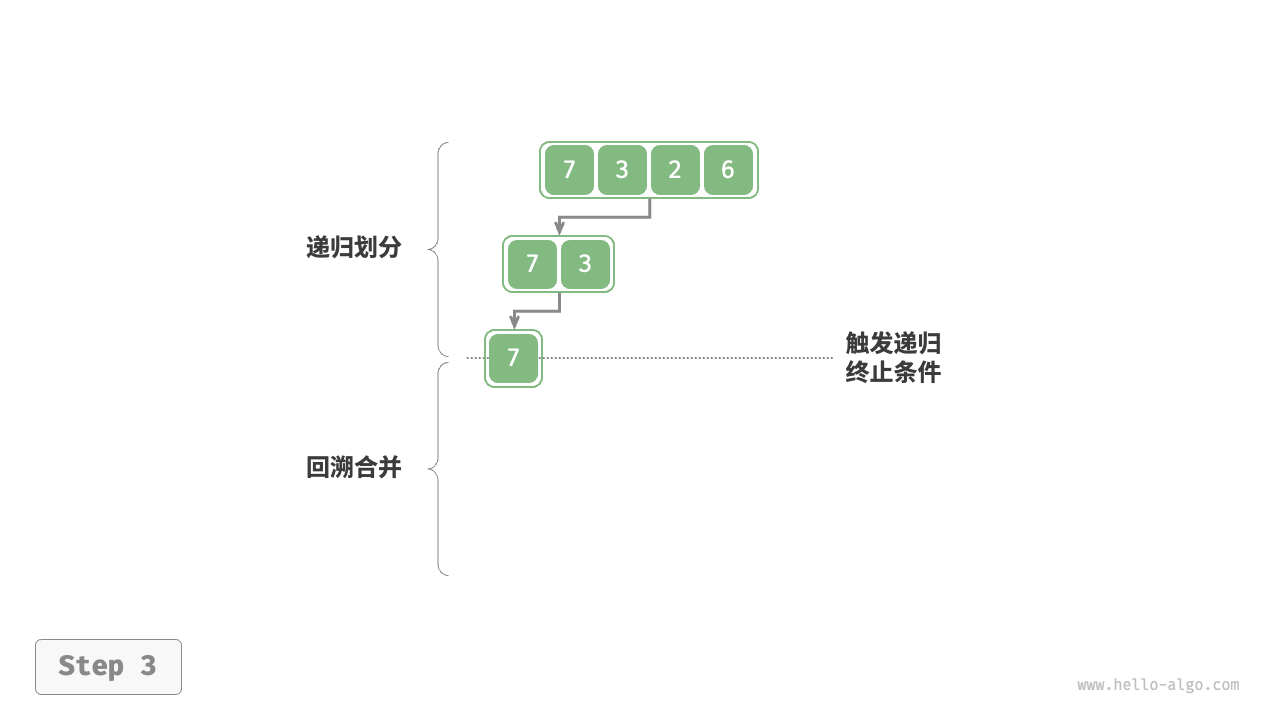
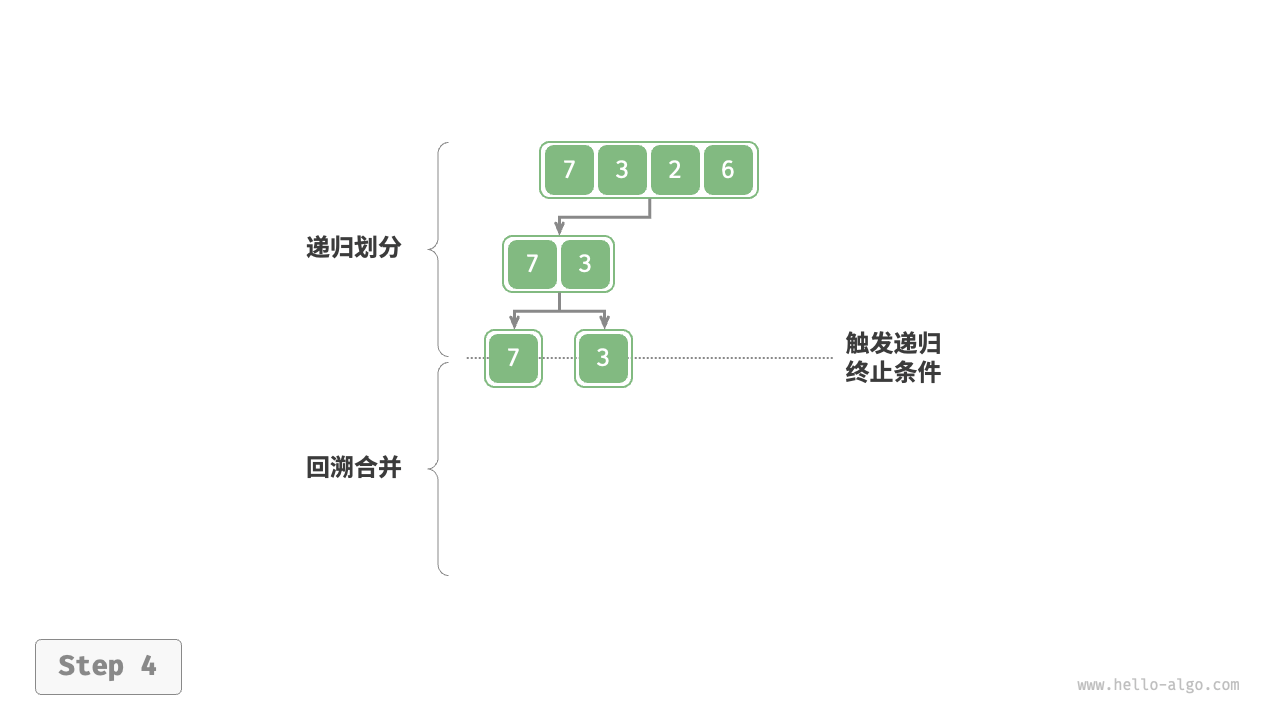
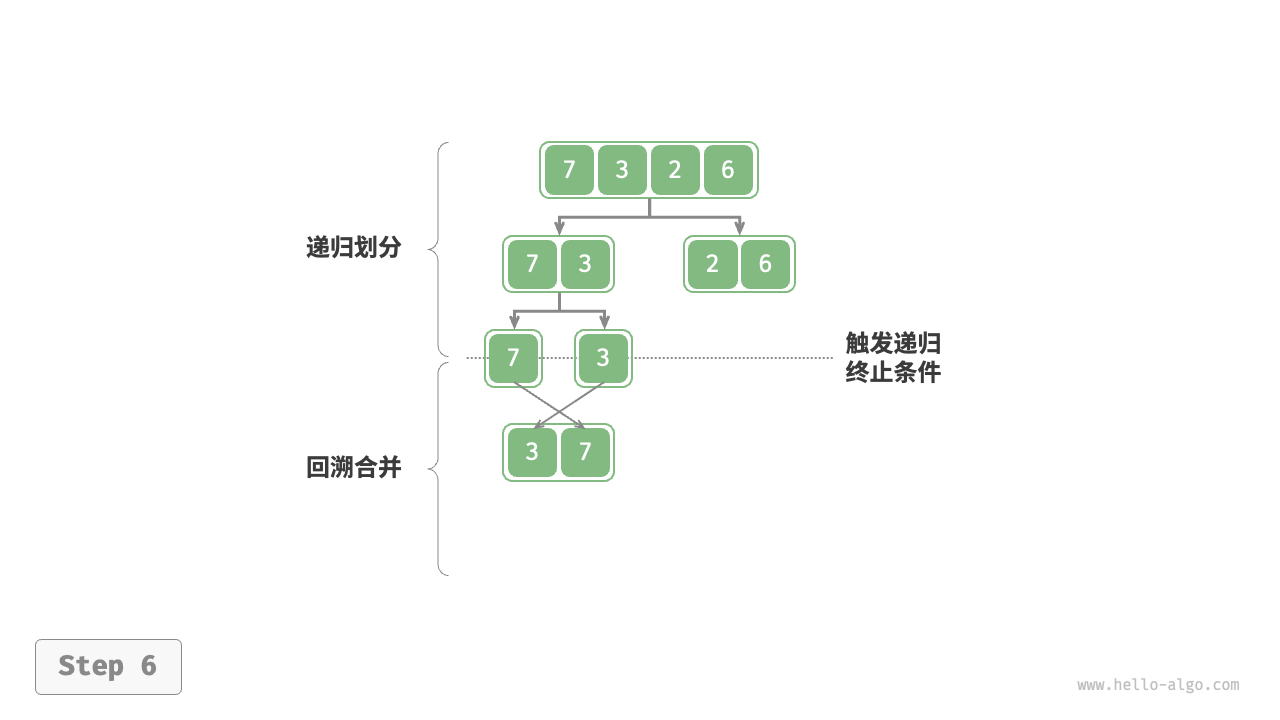
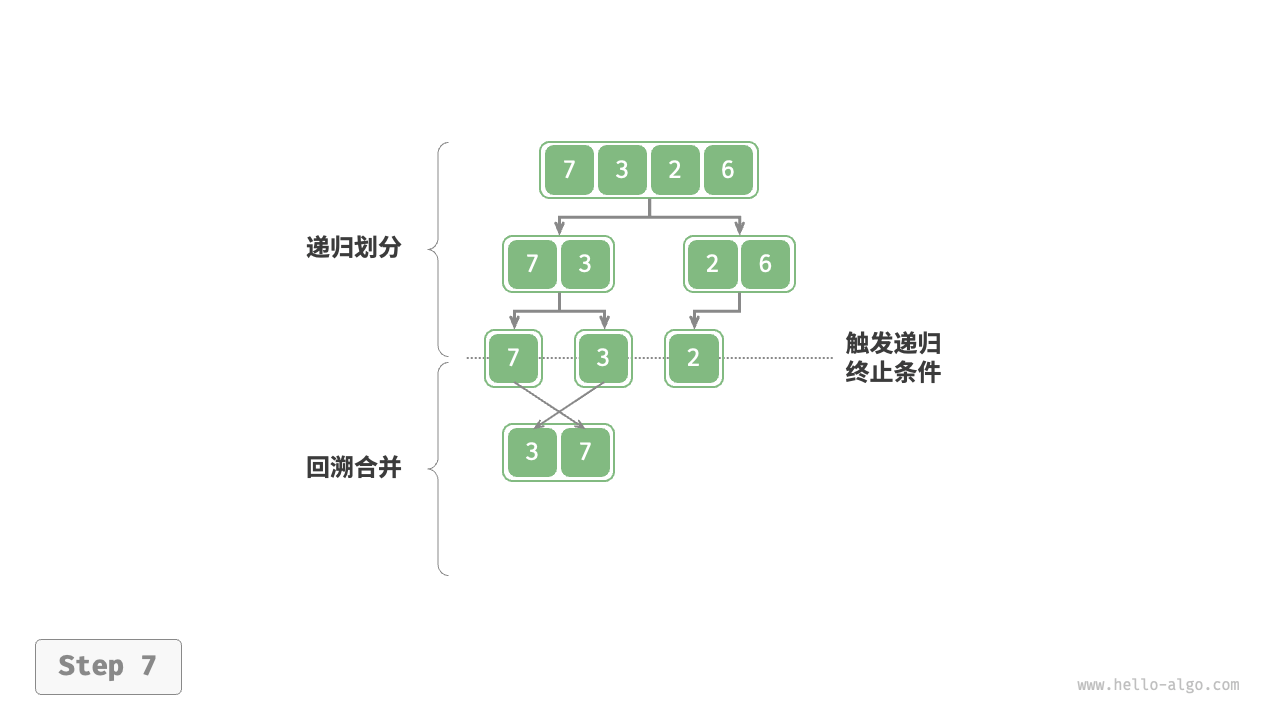
如下图所示,“划分阶段”从顶至底递归地将数组从中点切分为两个子数组。
- 计算数组中点
mid,递归划分左子数组(区间[left, mid])和右子数组(区间[mid + 1, right])。 - 递归执行步骤
1.,直至子数组区间长度为 1 时终止。
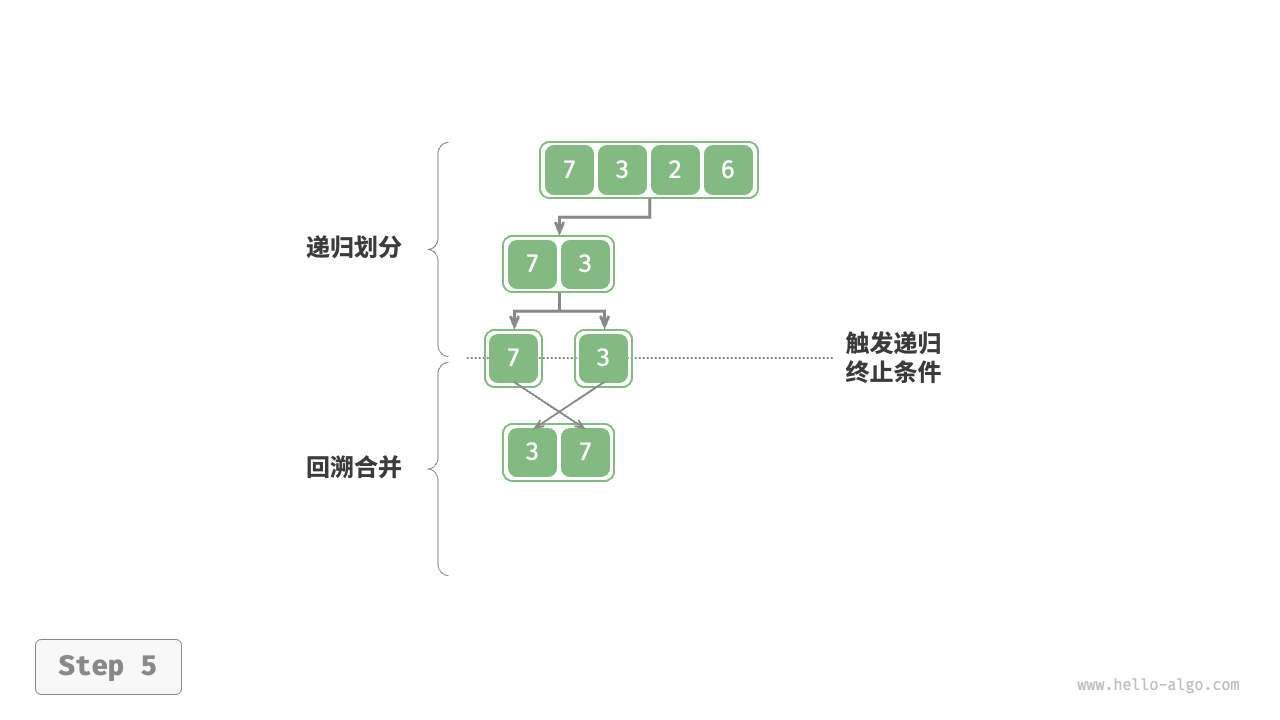
“合并阶段”从底至顶地将左子数组和右子数组合并为一个有序数组。需要注意的是,从长度为 1 的子数组开始合并,合并阶段中的每个子数组都是有序的。
观察发现,归并排序与二叉树后序遍历的递归顺序是一致的。
- 后序遍历:先递归左子树,再递归右子树,最后处理根节点。
- 归并排序:先递归左子数组,再递归右子数组,最后处理合并。
归并排序的实现如以下代码所示。请注意,nums 的待合并区间为 [left, right] ,而 tmp 的对应区间为 [0, right - left] 。
[file]{merge_sort}-[class]{}-[func]{merge_sort}
算法特性¶
- 时间复杂度为 $O(n \log n)$、非自适应排序:划分产生高度为 $\log n$ 的递归树,每层合并的总操作数量为 $n$ ,因此总体时间复杂度为 $O(n \log n)$ 。
- 空间复杂度为 $O(n)$、非原地排序:递归深度为 $\log n$ ,使用 $O(\log n)$ 大小的栈帧空间。合并操作需要借助辅助数组实现,使用 $O(n)$ 大小的额外空间。
- 稳定排序:在合并过程中,相等元素的次序保持不变。
链表排序¶
对于链表,归并排序相较于其他排序算法具有显著优势,可以将链表排序任务的空间复杂度优化至 $O(1)$ 。
- 划分阶段:可以使用“迭代”替代“递归”来实现链表划分工作,从而省去递归使用的栈帧空间。
- 合并阶段:在链表中,节点增删操作仅需改变引用(指针)即可实现,因此合并阶段(将两个短有序链表合并为一个长有序链表)无须创建额外链表。
具体实现细节比较复杂,有兴趣的读者可以查阅相关资料进行学习。