最大容量问题¶
Question
输入一个数组 $ht$ ,其中的每个元素代表一个垂直隔板的高度。数组中的任意两个隔板,以及它们之间的空间可以组成一个容器。
容器的容量等于高度和宽度的乘积(面积),其中高度由较短的隔板决定,宽度是两个隔板的数组索引之差。
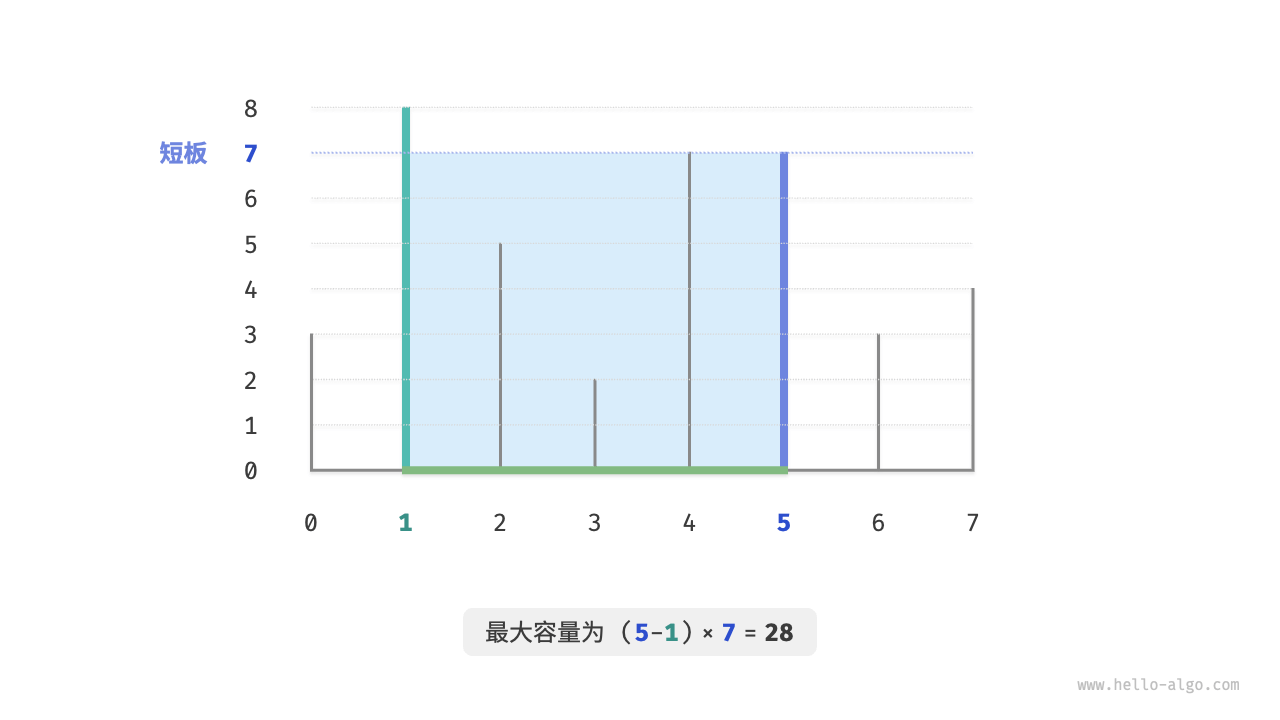
请在数组中选择两个隔板,使得组成的容器的容量最大,返回最大容量。示例如下图所示。
容器由任意两个隔板围成,因此本题的状态为两个隔板的索引,记为 $[i, j]$ 。
根据题意,容量等于高度乘以宽度,其中高度由短板决定,宽度是两隔板的数组索引之差。设容量为 $cap[i, j]$ ,则可得计算公式:
$$ cap[i, j] = \min(ht[i], ht[j]) \times (j - i) $$
设数组长度为 $n$ ,两个隔板的组合数量(状态总数)为 $C_n^2 = \frac{n(n - 1)}{2}$ 个。最直接地,我们可以穷举所有状态,从而求得最大容量,时间复杂度为 $O(n^2)$ 。
贪心策略确定¶
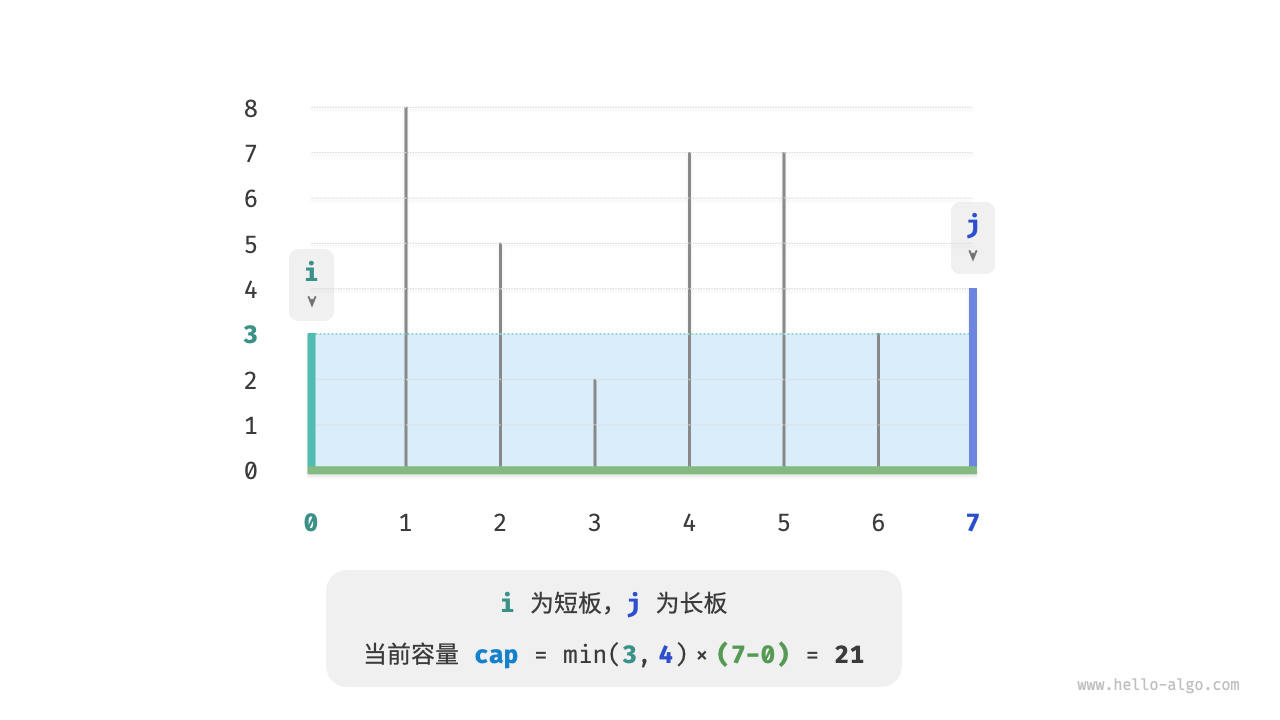
这道题还有更高效率的解法。如下图所示,现选取一个状态 $[i, j]$ ,其满足索引 $i < j$ 且高度 $ht[i] < ht[j]$ ,即 $i$ 为短板、$j$ 为长板。
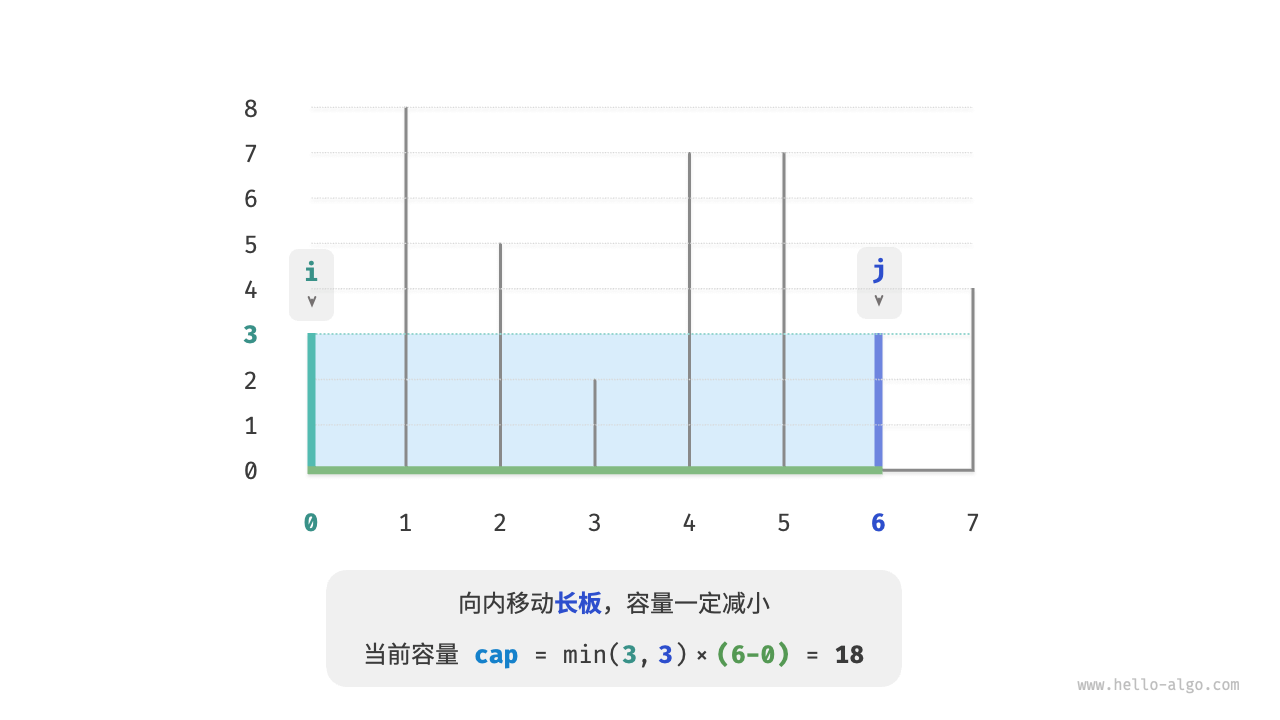
如下图所示,若此时将长板 $j$ 向短板 $i$ 靠近,则容量一定变小。
这是因为在移动长板 $j$ 后,宽度 $j-i$ 肯定变小;而高度由短板决定,因此高度只可能不变( $i$ 仍为短板)或变小(移动后的 $j$ 成为短板)。
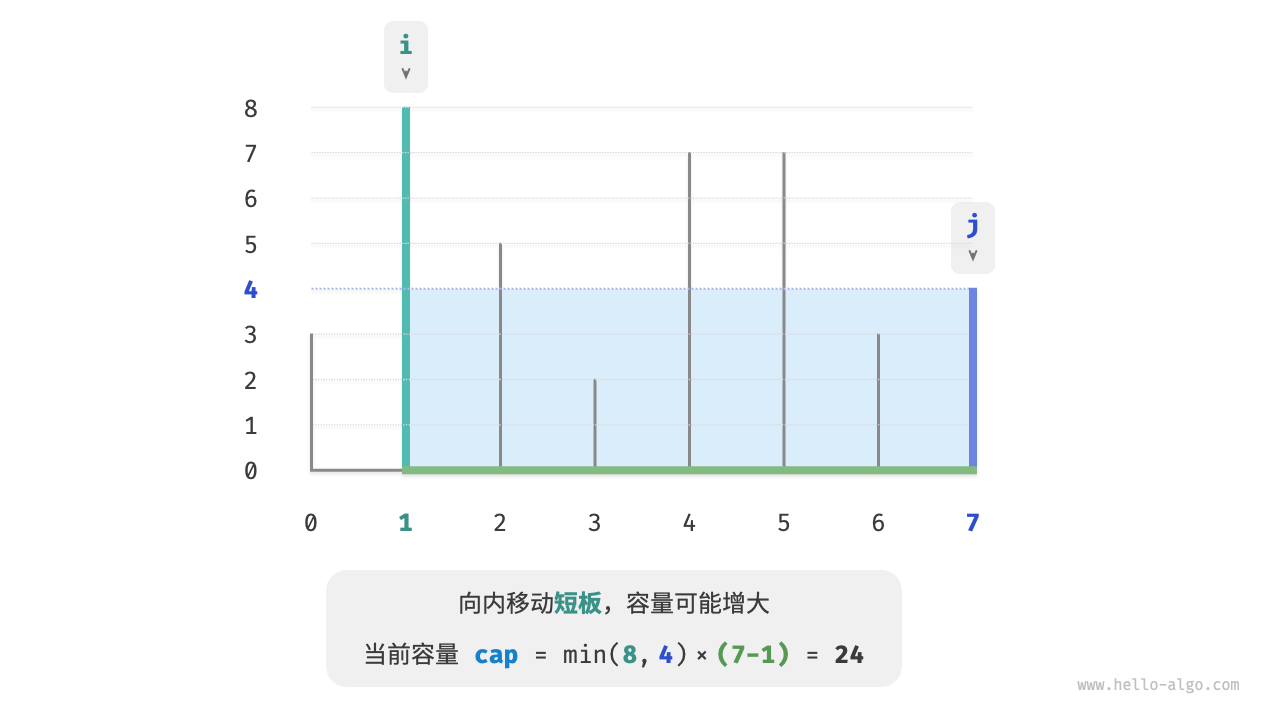
反向思考,我们只有向内收缩短板 $i$ ,才有可能使容量变大。因为虽然宽度一定变小,但高度可能会变大(移动后的短板 $i$ 可能会变长)。例如在下图中,移动短板后面积变大。
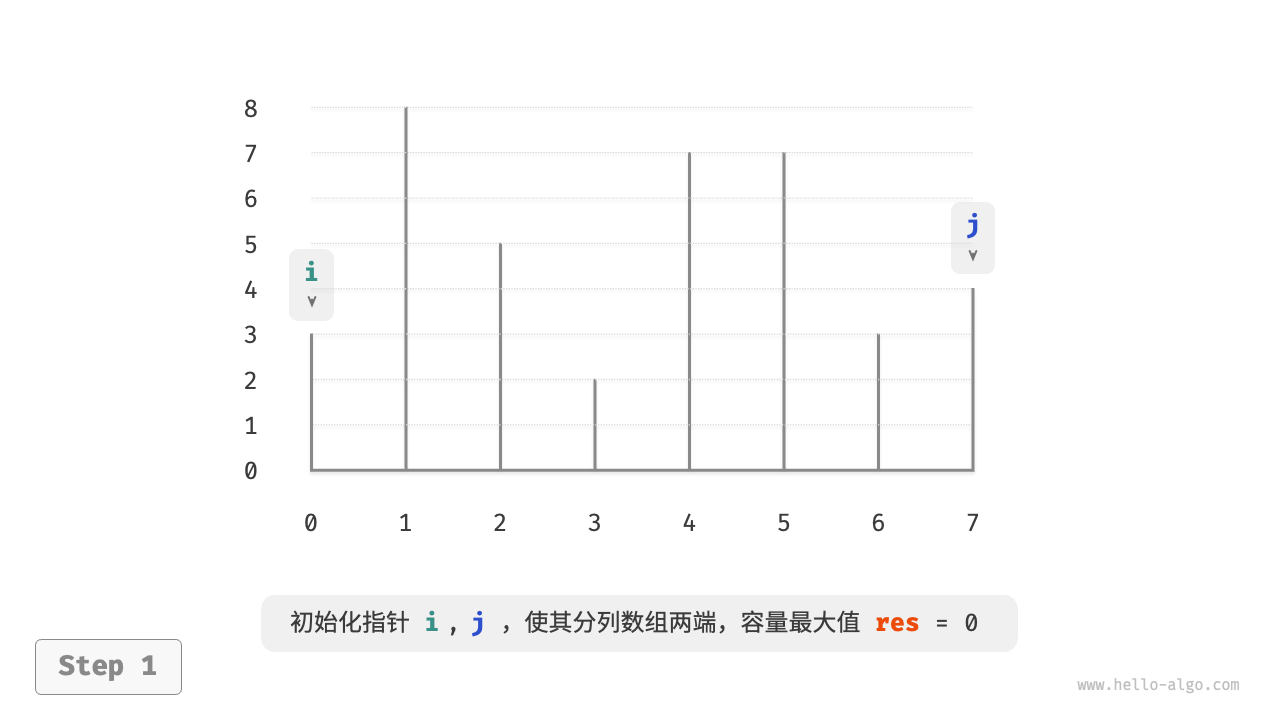
由此便可推出本题的贪心策略:初始化两指针,使其分列容器两端,每轮向内收缩短板对应的指针,直至两指针相遇。
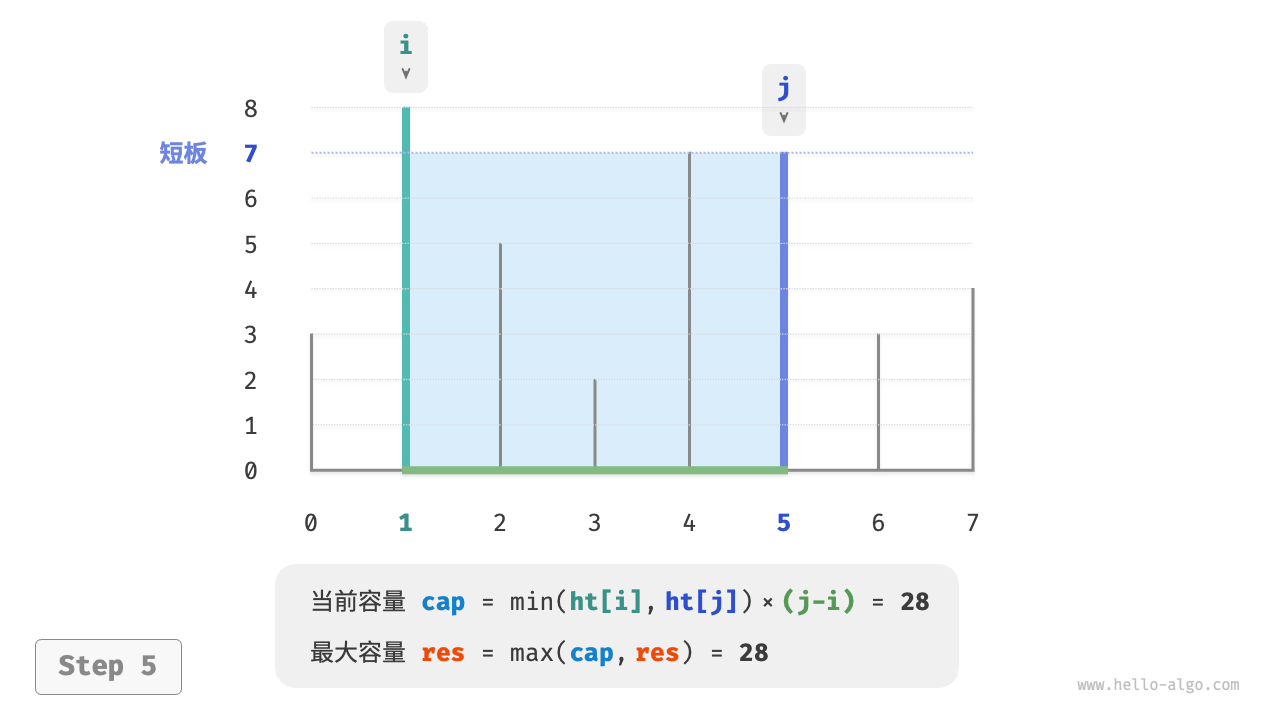
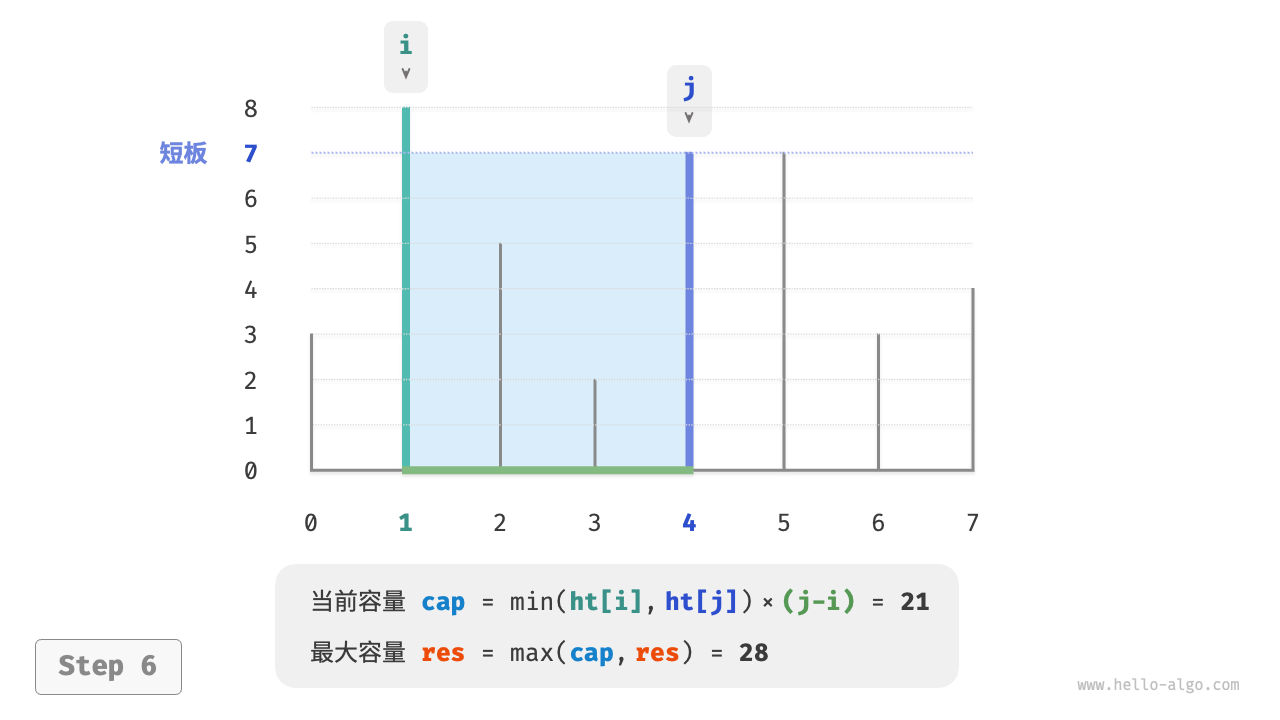
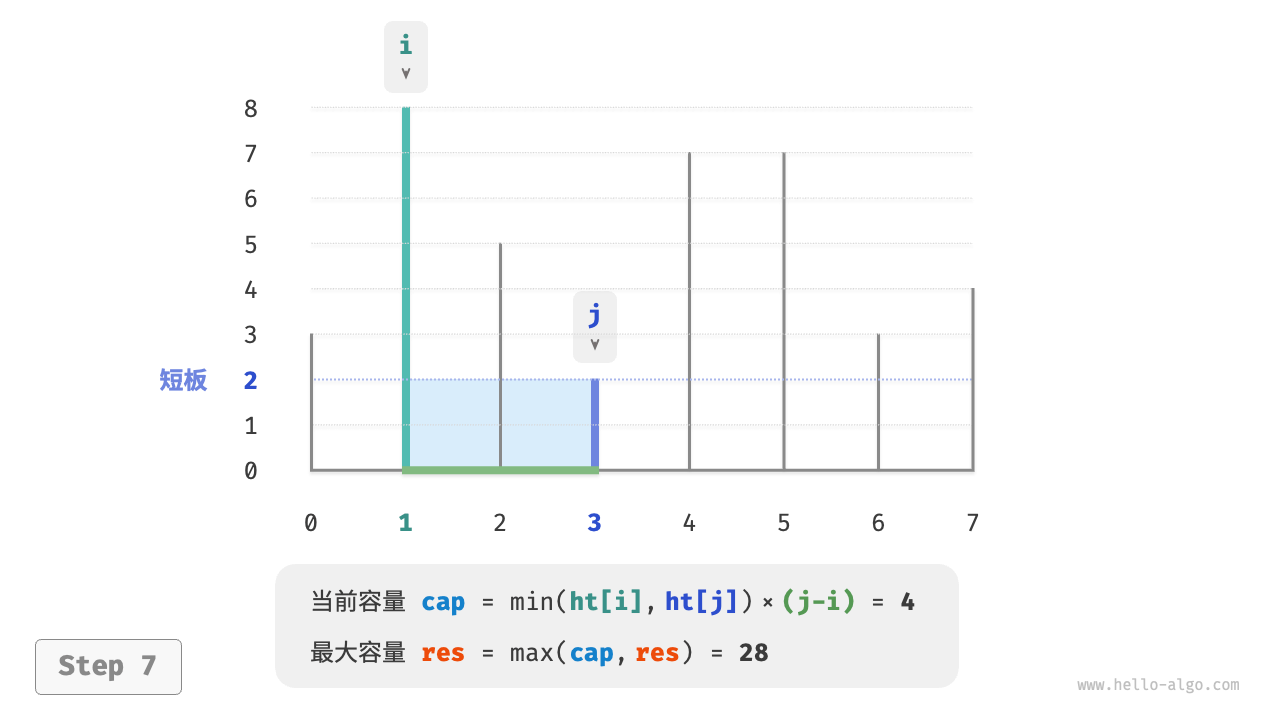
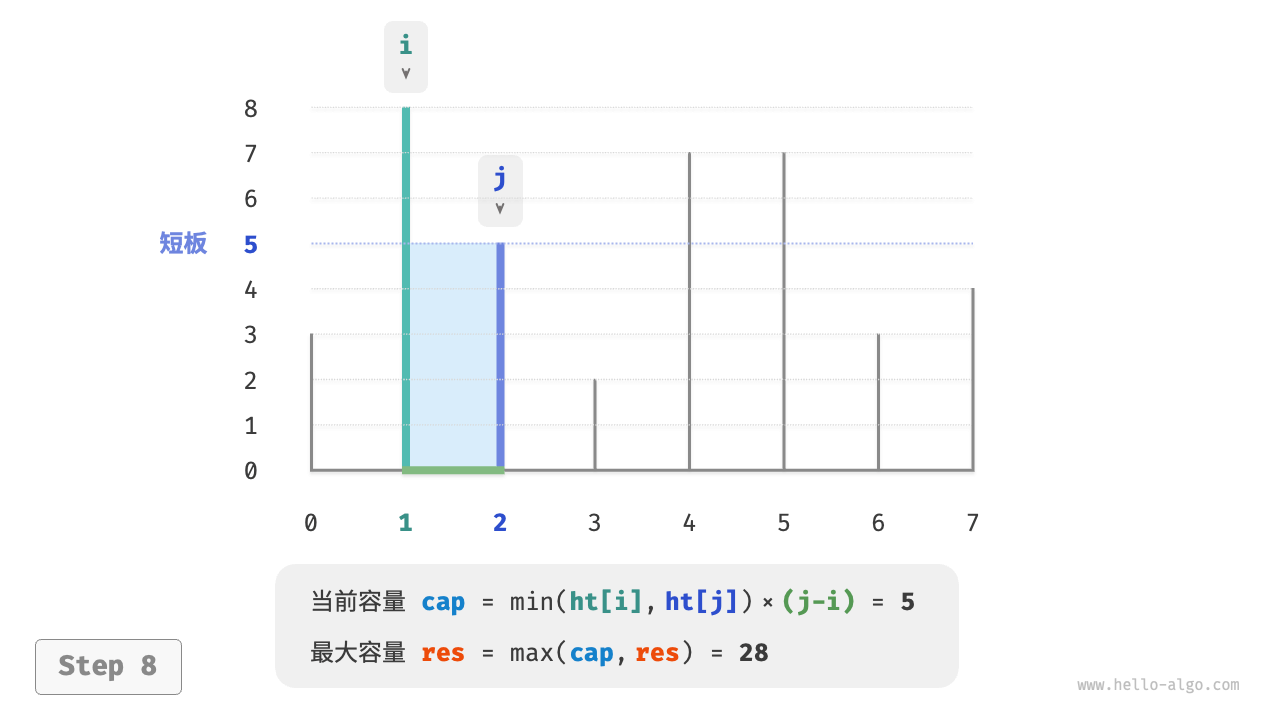
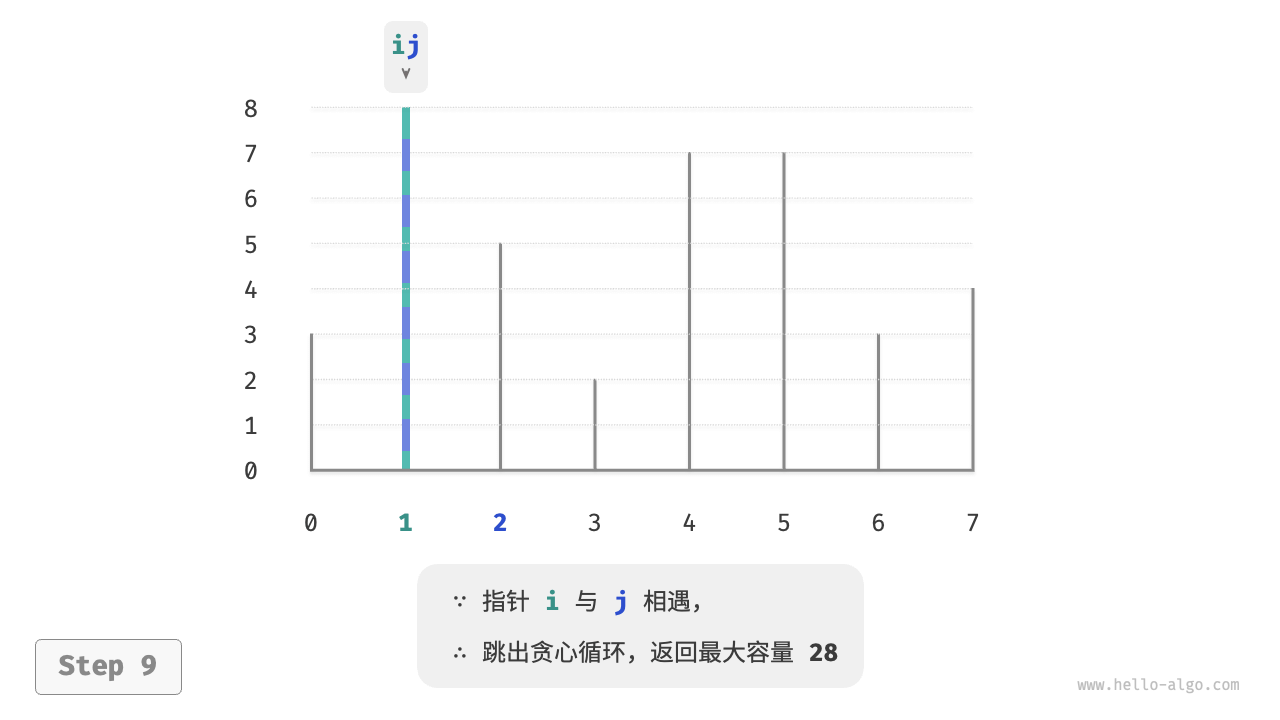
下图展示了贪心策略的执行过程。
- 初始状态下,指针 $i$ 和 $j$ 分列数组两端。
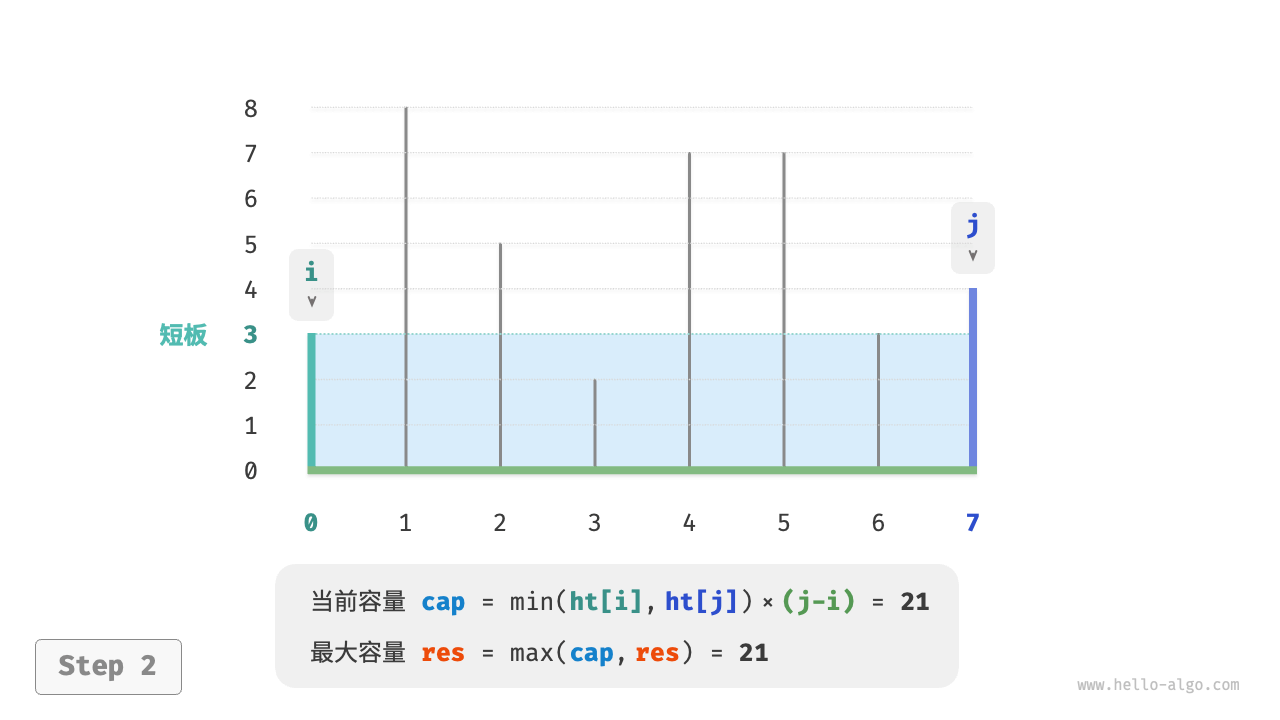
- 计算当前状态的容量 $cap[i, j]$ ,并更新最大容量。
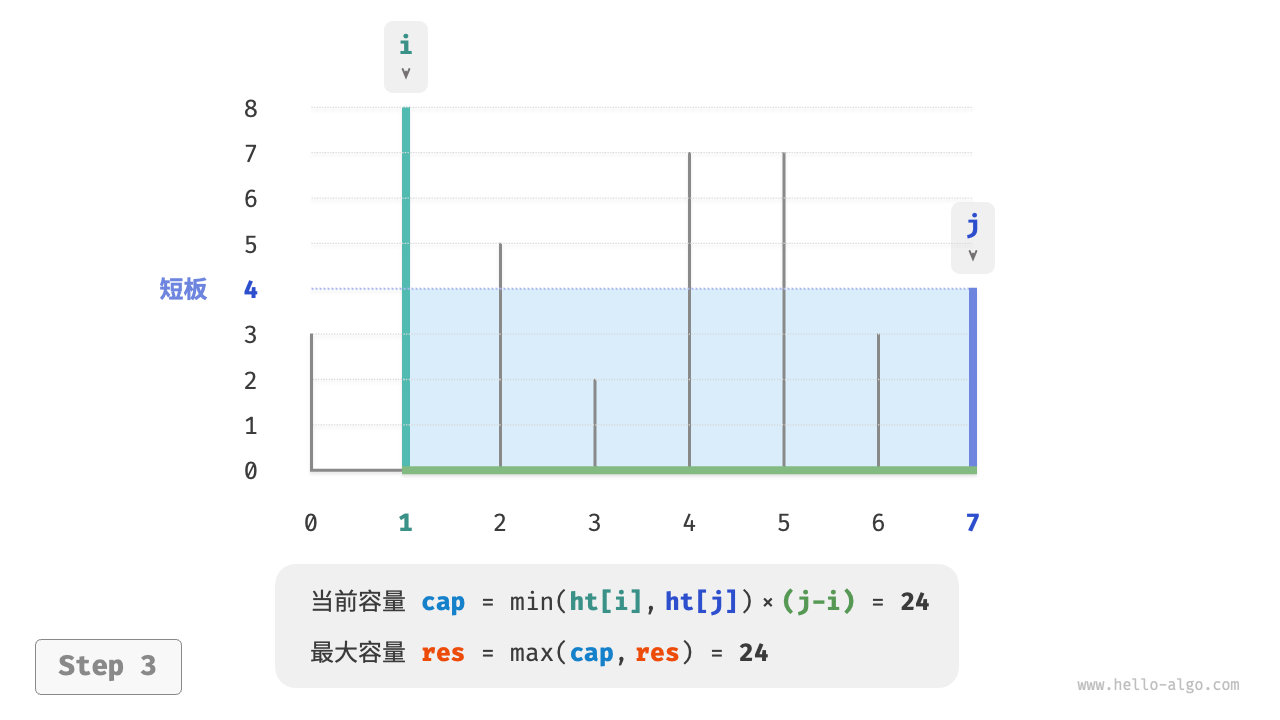
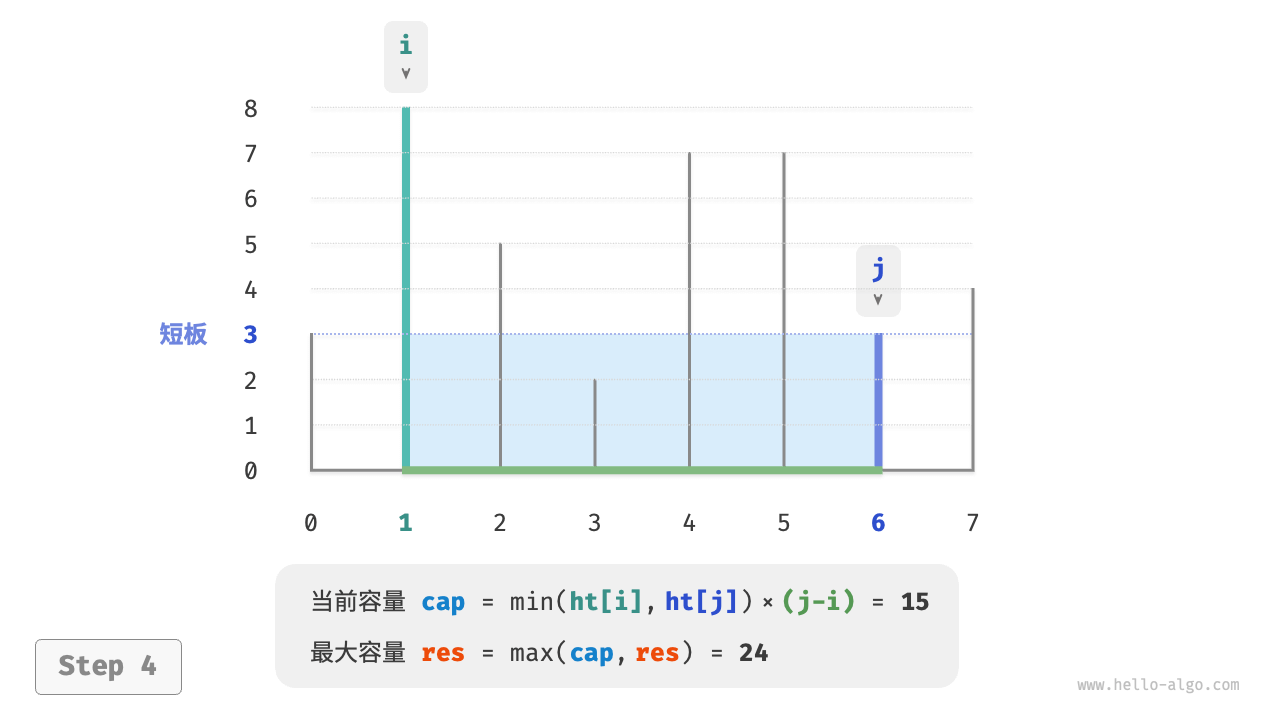
- 比较板 $i$ 和 板 $j$ 的高度,并将短板向内移动一格。
- 循环执行第
2.步和第3.步,直至 $i$ 和 $j$ 相遇时结束。
代码实现¶
代码循环最多 $n$ 轮,因此时间复杂度为 $O(n)$ 。
变量 $i$、$j$、$res$ 使用常数大小的额外空间,因此空间复杂度为 $O(1)$ 。
[file]{max_capacity}-[class]{}-[func]{max_capacity}
正确性证明¶
之所以贪心比穷举更快,是因为每轮的贪心选择都会“跳过”一些状态。
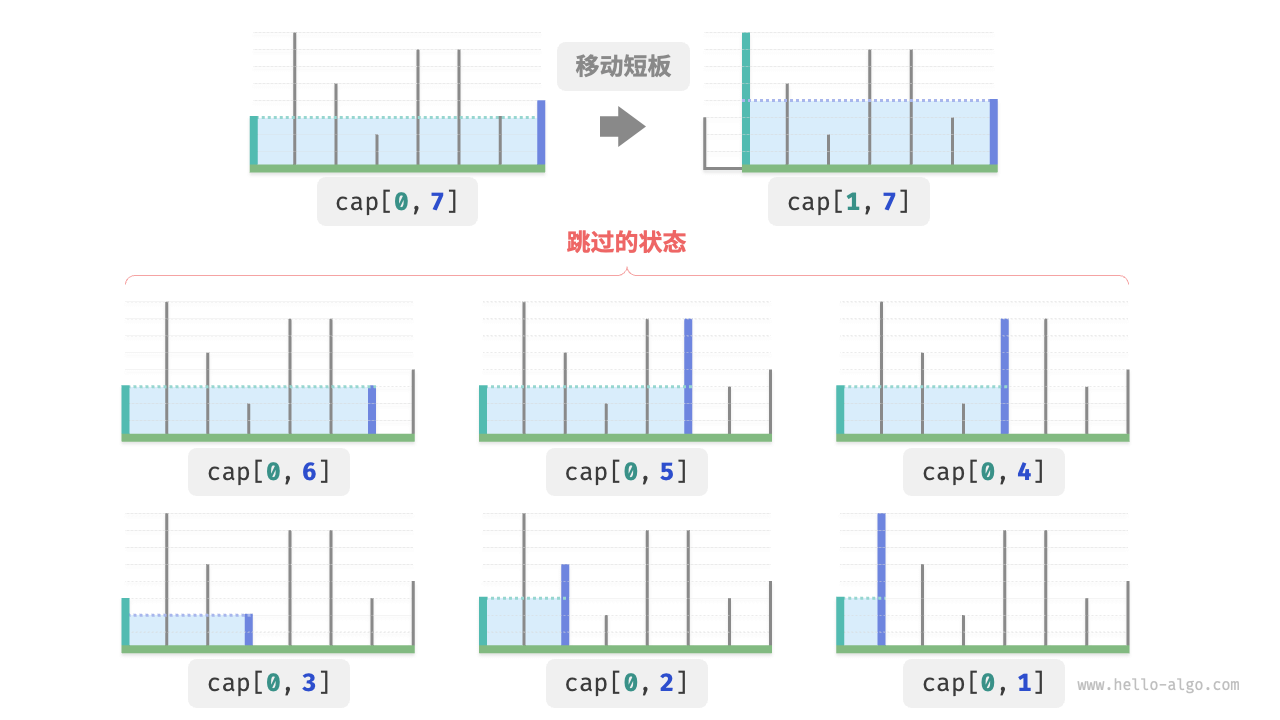
比如在状态 $cap[i, j]$ 下,$i$ 为短板、$j$ 为长板。若贪心地将短板 $i$ 向内移动一格,会导致下图所示的状态被“跳过”。这意味着之后无法验证这些状态的容量大小。
$$ cap[i, i+1], cap[i, i+2], \dots, cap[i, j-2], cap[i, j-1] $$
观察发现,这些被跳过的状态实际上就是将长板 $j$ 向内移动的所有状态。前面我们已经证明内移长板一定会导致容量变小。也就是说,被跳过的状态都不可能是最优解,跳过它们不会导致错过最优解。
以上分析说明,移动短板的操作是“安全”的,贪心策略是有效的。