基数排序¶
上一节介绍了计数排序,它适用于数据量 $n$ 较大但数据范围 $m$ 较小的情况。假设我们需要对 $n = 10^6$ 个学号进行排序,而学号是一个 $8$ 位数字,这意味着数据范围 $m = 10^8$ 非常大,使用计数排序需要分配大量内存空间,而基数排序可以避免这种情况。
基数排序(radix sort)的核心思想与计数排序一致,也通过统计个数来实现排序。在此基础上,基数排序利用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终的排序结果。
算法流程¶
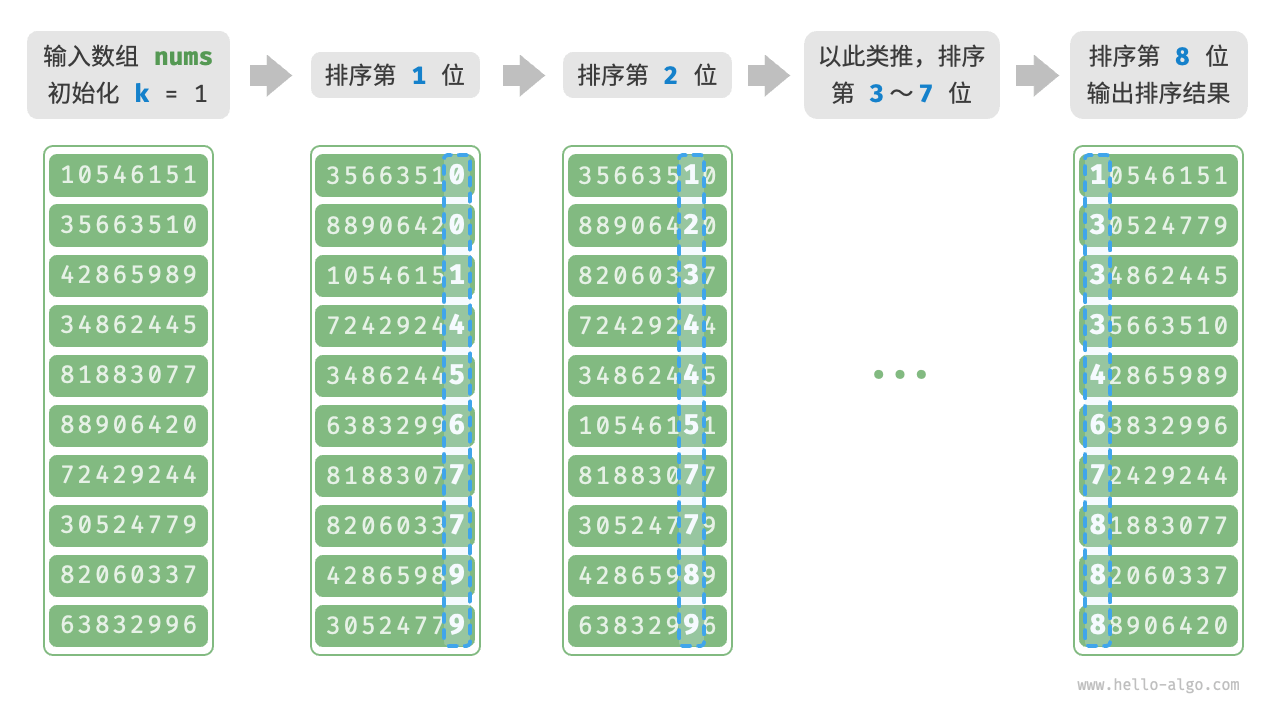
以学号数据为例,假设数字的最低位是第 $1$ 位,最高位是第 $8$ 位,基数排序的流程如下图所示。
- 初始化位数 $k = 1$ 。
- 对学号的第 $k$ 位执行“计数排序”。完成后,数据会根据第 $k$ 位从小到大排序。
- 将 $k$ 增加 $1$ ,然后返回步骤
2.继续迭代,直到所有位都排序完成后结束。
下面剖析代码实现。对于一个 $d$ 进制的数字 $x$ ,要获取其第 $k$ 位 $x_k$ ,可以使用以下计算公式:
$$ x_k = \lfloor\frac{x}{d^{k-1}}\rfloor \bmod d $$
其中 $\lfloor a \rfloor$ 表示对浮点数 $a$ 向下取整,而 $\bmod : d$ 表示对 $d$ 取模(取余)。对于学号数据,$d = 10$ 且 $k \in [1, 8]$ 。
此外,我们需要小幅改动计数排序代码,使之可以根据数字的第 $k$ 位进行排序:
[file]{radix_sort}-[class]{}-[func]{radix_sort}
为什么从最低位开始排序?
在连续的排序轮次中,后一轮排序会覆盖前一轮排序的结果。举例来说,如果第一轮排序结果 $a < b$ ,而第二轮排序结果 $a > b$ ,那么第二轮的结果将取代第一轮的结果。由于数字的高位优先级高于低位,因此应该先排序低位再排序高位。
算法特性¶
相较于计数排序,基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位数不能过大。例如,浮点数不适合使用基数排序,因为其位数 $k$ 过大,可能导致时间复杂度 $O(nk) \gg O(n^2)$ 。
- 时间复杂度为 $O(nk)$、非自适应排序:设数据量为 $n$、数据为 $d$ 进制、最大位数为 $k$ ,则对某一位执行计数排序使用 $O(n + d)$ 时间,排序所有 $k$ 位使用 $O((n + d)k)$ 时间。通常情况下,$d$ 和 $k$ 都相对较小,时间复杂度趋向 $O(n)$ 。
- 空间复杂度为 $O(n + d)$、非原地排序:与计数排序相同,基数排序需要借助长度为 $n$ 和 $d$ 的数组
res和counter。 - 稳定排序:当计数排序稳定时,基数排序也稳定;当计数排序不稳定时,基数排序无法保证得到正确的排序结果。